
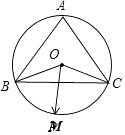
【题目】在△ABC中,∠A= ![]() ,O为平面内一点.且|
,O为平面内一点.且| ![]() |,M为劣弧
|,M为劣弧 ![]() 上一动点,且
上一动点,且 ![]() .则p+q的取值范围为 .
.则p+q的取值范围为 .
【答案】[1,2]
【解析】解:如图所示,△ABC中,∠A= ![]() ,∴∠BOC=
,∴∠BOC= ![]() ;
;
设| ![]() =r,则O为△ABC外接圆圆心;
=r,则O为△ABC外接圆圆心;
∵ ![]() =p
=p ![]() +q
+q ![]() ,
,
∴ ![]() =
= ![]() =r2,
=r2,
即p2r2+q2r2+2pqr2cos ![]() =r2,
=r2,
∴p2+q2﹣pq=1,
∴(p+q)2=3pq+1;
又M为劣弧AC上一动点,
∴0≤p≤1,0≤q≤1,
∴p+q≥2 ![]() ,
,
∴pq≤ ![]() =
= ![]() ,
,
∴1≤(p+q)2≤ ![]() (p+q)2+1,
(p+q)2+1,
解得1≤(p+q)2≤4,
∴1≤p+q≤2;
即p+q的取值范围是[1,2].
所以答案是:[1,2].
【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案,需要熟知如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 分成左右两部分,在PQ 左侧部分三角形POQ 为观赏区,在PQ 右侧部分种草,已知种花的单位面积的造价为3a,种草的单位面积的造价为2a,其中a 为正常数,设∠AOP=θ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,设总造价为f(θ) 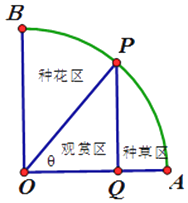
(1)求f(θ)关于θ 的函数关系式;
(2)求当θ 为何值时,总造价最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设 ![]() (α,β∈R),则α+β的取值范围是 .
(α,β∈R),则α+β的取值范围是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角分别为A,B,C,且a>c.已知△ABC的面积为 ![]() ,
, ![]() ,b=3.
,b=3.
(Ⅰ)求a,c的值;
(Ⅱ)求sin(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x1 , x2 , x3 , x4},xi∈{﹣1,0,1},i={1,2,3,4},那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为( )
A.60
B.65
C.80
D.81
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+a)ln(x+a),g(x)=﹣ ![]() +ax.
+ax.
(1)函数h(x)=f(ex﹣a)+g'(ex),x∈[﹣1,1],求函数h(x)的最小值;
(2)对任意x∈[2,+∞),都有f(x﹣a﹣1)﹣g(x)≤0成立,求a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx.若存在x1 , x2 , ,xm满足0≤x1<x2<<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|++|f(xm﹣1)﹣f(xm)|=12(m≥2,m∈N*),则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0).
|+|x﹣2m|(m>0).
(Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com