
����Ŀ����ͼ��һ��Բ�Ľ�Ϊֱ�ǵ�����AOB ���ݷ����뾶Ϊ1����P �ǻ��ݷ�����һ�����㣬�����˵㣬�ִ���������BOP ���ֻ���PQ��OA������ΪQ��PQ ������AOP �ֳ����������֣���PQ ��ಿ��������POQ Ϊ����������PQ �Ҳಿ���ֲݣ���֪�ֻ��ĵ�λ��������Ϊ3a���ֲݵĵ�λ��������Ϊ2a������a Ϊ�����������AOP=�ȣ��ֻ���������ֲݵ���۵ĺͳ�Ϊ����ۣ����ƹ���������ۣ��������Ϊf���ȣ� 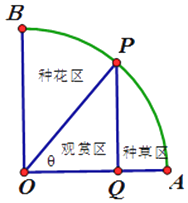
��1����f���ȣ����ڦ� �ĺ�����ϵʽ��
��2���� Ϊ��ֵʱ���������С���������Сֵ��
���𰸡�
��1���⣺�ֻ��������Ϊ ![]() ���ֲ��������Ϊ
���ֲ��������Ϊ ![]() ��
��
�������f���ȣ�= ![]() ��
�� ![]() ���ȣ�+��
���ȣ�+�� ![]() ��
�� ![]() sin��cos�ȣ�2��=��
sin��cos�ȣ�2��=�� ![]() ��
�� ![]() ��sin��cos�ȣ�����0���ȣ�
��sin��cos�ȣ�����0���ȣ� ![]()
��2���⣺ ![]() =
= ![]()
��f'���ȣ�=0���õ� ![]()
�� | | | |
f'���ȣ� | _ | 0 | + |
f���ȣ� | �ݼ� | ��Сֵ | ���� |
�ʵ� ![]() ʱ���������С�����������СΪ
ʱ���������С�����������СΪ 
����������1���ֱ�����ֻ�������ۣ��ֲ�������ۣ����ɵõ�f���ȣ����ڦ� �ĺ�����ϵʽ����2�������ٸ��ݵ����ͺ�������ֵ�ù�ϵ��������𰸣�
�����㾫�������ڱ��⿼������������ʽ����Ҫ�˽������ε�Բ�Ľ�Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() ������Ϊ
������Ϊ![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ���ܵó���ȷ�𰸣�
���ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ������a��b��c��R��
������a��b��c��R��
������a=b=1������f��x���ĵ������䣻
������a=0���ҵ�x��0ʱ��f��x����1�ܳ�������ʵ��b��ȡֵ��Χ��
������a��0��b=0����f��x������������ֵ��x1 �� x2 �� ��֤��f��x1��+f��x2����e��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A��B��C��D��E��FΪ����Ķ������У��ı���ACDF�����Σ���FAC=60�㣬AB��DE��BC��EF��AB=BC=3��AF=2 ![]() ��
�� 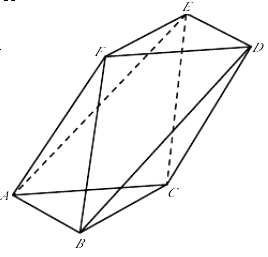
��1����֤��ƽ��ABC��ƽ��ACDF��
��2����ƽ��AEF��ƽ��ACE���ɵ������ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��������f��x�������ֵM����M��ȡֵ��Χ�ǣ� ��
��������f��x�������ֵM����M��ȡֵ��Χ�ǣ� ��
A.�� ![]() ��0��
��0��
B.��0�� ![]() ]
]
C.��0�� ![]() ]
]
D.�� ![]() ��
�� ![]() ]
]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵԭ��OΪ���㣬x��������Ϊ���ᣬ��֪����C1�IJ�������Ϊ ![]() ��tΪ��������C2�ļ����귽��Ϊ��2��1+sin2�ȣ�=8��C3�ļ����귽��Ϊ��=��������[0���У����ѡ�R��
��tΪ��������C2�ļ����귽��Ϊ��2��1+sin2�ȣ�=8��C3�ļ����귽��Ϊ��=��������[0���У����ѡ�R��
��1����C1��C3��һ��������ΪA������O�㣩����|OA|= ![]() �������
�������
��2����C1��C3��һ��������ΪA������O�㣩��C2��C3��һ��������ΪB����|OA||OB|��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪�� ![]() ��tΪ�����������Բ
��tΪ�����������Բ ![]() ����Ϊ���������ҽ���F��
����Ϊ���������ҽ���F��
��1����m��ֵ��
��2����ֱ��l����ԲC����A��B���㣬��|FA||FB|�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��������ABCD��A1B1C1D1�ĶԽ���BD1�ϣ�����P����ֱ��ƽ��BB1D1D��ֱ�ߣ�������������ཻ��M��N����BP=x��MN=y������y=f��x����ͼ������ǣ� �� 
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}�ǹ������0�ĵȲ����У�SnΪ����{an}��ǰn��ͣ���֪S3=9����2a1 �� a3��1��a4+1���ɵȱ����У�
��1��������{an}��ͨ�ʽ��
��2��������{bn}���� ![]() =2n��1��n��N*������Tn������{bn}��ǰn��ͣ�֤����Tn��6��
=2n��1��n��N*������Tn������{bn}��ǰn��ͣ�֤����Tn��6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A= ![]() ��OΪƽ����һ�㣮��|
��OΪƽ����һ�㣮��| ![]() |��MΪ�ӻ�
|��MΪ�ӻ� ![]() ��һ���㣬��
��һ���㣬�� ![]() ����p+q��ȡֵ��ΧΪ ��
����p+q��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com