
【题目】以直角坐标系原点O为极点,x轴正方向为极轴,已知曲线C1的参数方程为 ![]() (t为参数),C2的极坐标方程为ρ2(1+sin2θ)=8,C3的极坐标方程为θ=α,α∈[0,π),ρ∈R,
(t为参数),C2的极坐标方程为ρ2(1+sin2θ)=8,C3的极坐标方程为θ=α,α∈[0,π),ρ∈R,
(1)若C1与C3的一个公共点为A(异于O点),且|OA|= ![]() ,求α;
,求α;
(2)若C1与C3的一个公共点为A(异于O点),C2与C3的一个公共点为B,求|OA||OB|的取值范围.
【答案】
(1)解:曲线C1的参数方程为 ![]() (t为参数),则直角方程为(x﹣1)2+y2=1,
(t为参数),则直角方程为(x﹣1)2+y2=1,
极坐标方程为ρ=2cosθ,联立极坐标方程 ![]() ,得
,得  ,
,
由|OA|= ![]() =丨ρ1﹣ρ2丨=丨2cosα丨,
=丨ρ1﹣ρ2丨=丨2cosα丨,
解得cosα=± ![]() ,则α=
,则α= ![]() 或α=
或α= ![]() .
.
(2)解:联立C1与C3的极坐标方程为  ,丨OB丨=丨ρ丨=
,丨OB丨=丨ρ丨= ![]() ,
,
当α= ![]() 时,O与A重合,所以α≠
时,O与A重合,所以α≠ ![]() ,则
,则
|OA||OB|=丨2cosα丨 ![]() =4
=4 ![]() =4
=4 ![]() =4
=4 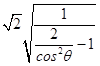 ,
,
∴|OA||OB|∈(0,4 ![]() ],
],
|OA||OB|的取值范围∈(0,4 ![]() ].
].
【解析】(1)由曲线C1的参数方程求得直角坐标方程,即可求得极坐标方程,与曲线C3联立,即可求得ρ1,ρ2,由|OA|=丨ρ1﹣ρ2丨,即可求得α;(2)联立C1与C3的极坐标方程.即可求得丨OB丨,则|OA||OB|=丨2cosα丨 ![]() ,化简即可求得|OA||OB|的取值范围.
,化简即可求得|OA||OB|的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4lnx﹣x+![]() , g(x)=2x2﹣bx+20,若对于任意x1∈(0,2),都存在x2∈[1,2],使得f(x1)≥g(x2)成立,则实数b的取值范围是
, g(x)=2x2﹣bx+20,若对于任意x1∈(0,2),都存在x2∈[1,2],使得f(x1)≥g(x2)成立,则实数b的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1,g(x)=lnx﹣ax+a,若存在x0∈(1,2),使得f(x0)g(x0)<0,则实数a的取值范围是( )
A.![]()
B.(ln2,e﹣1)
C.[1,e﹣1)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx﹣xcosx(x≥0).
(1)求函数f(x)的图象在 ![]() 处的切线方程;
处的切线方程;
(2)若任意x∈[0,+∞),不等式f(x)<ax3恒成立,求实数a的取值范围;
(3)设m=![]() f(x)dx,
f(x)dx, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且S5=a5+a6=25.
(1)求{an}的通项公式;
(2)若不等式2Sn+8n+27>(﹣1)nk(an+4)对所有的正整数n都成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP 分成左右两部分,在PQ 左侧部分三角形POQ 为观赏区,在PQ 右侧部分种草,已知种花的单位面积的造价为3a,种草的单位面积的造价为2a,其中a 为正常数,设∠AOP=θ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,设总造价为f(θ) 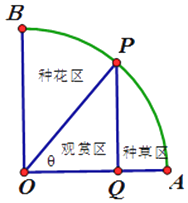
(1)求f(θ)关于θ 的函数关系式;
(2)求当θ 为何值时,总造价最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过M的直线与抛物线交于A,B两点.设A(x1 , y1)到准线l的距离为d,且d=λp(λ>0). 
(1)若y1=d=1,求抛物线的标准方程;
(2)若 ![]() +λ
+λ ![]() =
= ![]() ,求证:直线AB的斜率为定值.
,求证:直线AB的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,错误的是( )
A.若p为真,则¬(¬p)也为真
B.若“p∧q为真”,则“p∨q为真”为真命题
C.x∈R,使得tanx=2017
D.“2x> ![]() ”是“log
”是“log ![]() x<0”的充分不必要条件
x<0”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x1 , x2 , x3 , x4},xi∈{﹣1,0,1},i={1,2,3,4},那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为( )
A.60
B.65
C.80
D.81
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com