
【题目】已知函数f(x)=sinx﹣xcosx(x≥0).
(1)求函数f(x)的图象在 ![]() 处的切线方程;
处的切线方程;
(2)若任意x∈[0,+∞),不等式f(x)<ax3恒成立,求实数a的取值范围;
(3)设m=![]() f(x)dx,
f(x)dx, ![]() ,证明:
,证明: ![]() .
.
【答案】
(1)解:∵f′(x)=xsinx, ![]() ,
,
∴切线为 ![]() ;
;
(2)解:f(x)≤ax3sinx﹣xcosx﹣ax3≤0,
令g(x)=sinx﹣xcosx﹣ax3,
则g′(x)=xsinx﹣3ax2=x(sinx﹣3ax),
又令h(x)=sinx﹣3axh′(x)=cosx﹣3a,
①当3a≤﹣1,即 ![]() 时,h′(x)≥0恒成立,∴h(x)递增,
时,h′(x)≥0恒成立,∴h(x)递增,
∴h(x)≥h(0)=0,∴g′(x)≥0,∴g(x)递增,
∴g(x)≥g(0)=0(不合题意);
②当3a≥1即 ![]() 时,h′(x)≤0h(x)递减,
时,h′(x)≤0h(x)递减,
∴h(x)≤h(0)=0,∴g′(x)≤0,∴g(x)递减
∴g(x)≤g(0)=0(符合题意)
③当﹣1<3a<1,即 ![]() 时,
时,
由h′(0)=1﹣3a>0h′(π)=﹣1﹣3a<0,
∴在(0,π)上,x0,使h′(x0)=0
且x∈(0,x0)时,h′(x)>0g′(x)>0,
∴g(x)递增,∴g(x)>g(0)=0(不符合题意)
综上: ![]() .
.
(3)解: 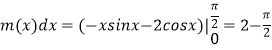
∴ ![]() ,由(1)知,当
,由(1)知,当 ![]() 时,
时, ![]() ,∴g(x)≤x,
,∴g(x)≤x,
又令μ(x)=ln(1+x)﹣x,x>0 ![]() ,
,
∴u(x)递减u(x)<u(0)=0,
即ln(1+x)<x在(0,+∞)上恒成立,
令 ![]() ,
,
∴原不等式 ![]() ,
,
∴左式 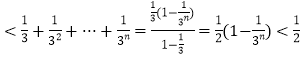 =右式
=右式
∴得证.
【解析】(1)求出函数的导数,计算f′( ![]() )的值,求出切线方程即可;(2)令g(x)=sinx﹣xcosx﹣ax3,求出函数的导数,令h(x)=sinx﹣3ax,通过讨论a的范围,结合函数的单调性求出a的范围即可;(3)求出g(x)的解析式,求出ln(1+x)<x在(0,+∞)上恒成立,令
)的值,求出切线方程即可;(2)令g(x)=sinx﹣xcosx﹣ax3,求出函数的导数,令h(x)=sinx﹣3ax,通过讨论a的范围,结合函数的单调性求出a的范围即可;(3)求出g(x)的解析式,求出ln(1+x)<x在(0,+∞)上恒成立,令 ![]() ,累加即可.
,累加即可.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】设常数a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,则a的取值范围为( )
A.(﹣∞,2)
B.(﹣∞,2]
C.(2,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标. 某市环保局从市区2016年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
(Ⅰ)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(Ⅱ)从这15天的数据中任取3天的数据,记ξ表示其中空气质量达到一级的天数,求ξ的分布列;
(Ⅲ)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2 ![]() .
. 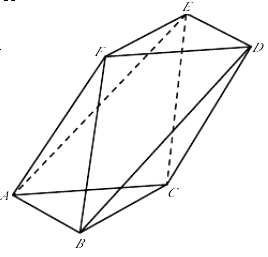
(1)求证:平面ABC⊥平面ACDF;
(2)求平面AEF与平面ACE所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系原点O为极点,x轴正方向为极轴,已知曲线C1的参数方程为 ![]() (t为参数),C2的极坐标方程为ρ2(1+sin2θ)=8,C3的极坐标方程为θ=α,α∈[0,π),ρ∈R,
(t为参数),C2的极坐标方程为ρ2(1+sin2θ)=8,C3的极坐标方程为θ=α,α∈[0,π),ρ∈R,
(1)若C1与C3的一个公共点为A(异于O点),且|OA|= ![]() ,求α;
,求α;
(2)若C1与C3的一个公共点为A(异于O点),C2与C3的一个公共点为B,求|OA||OB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上.过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图: 
(1)某同学不小心把茎叶图中的一个数字弄污了,看不清了,在如图所示的茎叶图中用m表示,若甲运动员成绩的中位数是33,求m的值;
(2)估计乙运动员在这次季后赛比赛中得分落在[20,40]内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com