
【题目】如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设 ![]() (α,β∈R),则α+β的取值范围是 .
(α,β∈R),则α+β的取值范围是 . 
【答案】(1,![]() )
)
【解析】解:以AB为x轴,以AD为y轴,建立坐标系,
∵在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3
∴A(0,0),D(0,1),B(3,0),C(1,1)
∴直线BD的方程为:y=﹣ ![]() x+1,即x+3y﹣3=0,
x+1,即x+3y﹣3=0,
C(1,1)点到直线的距离为: ![]()
∴以点C为圆心,且与直线BD相切的圆的方程为:
(x﹣1)2+(y﹣1)2= ![]() ,x=1+
,x=1+ ![]() cosθ,y=1+
cosθ,y=1+ ![]() sinθ
sinθ
设P(x,y)则:(x﹣1)2+(y﹣1)2≤ ![]() ,
,
∵ ![]() ,(α,β∈R),
,(α,β∈R),
∴(x,y)=(3β,α)
∴α+β=y+ ![]() =1+
=1+ ![]() sinθ
sinθ ![]() +
+ ![]() (1+
(1+ ![]() cosθ)=
cosθ)= ![]() +
+ ![]() cosθ+
cosθ+ ![]() sinθ=
sinθ= ![]() +
+ ![]() sin(θ+λ)
sin(θ+λ)
∵﹣ ![]() <
< ![]() sin(θ+λ)
sin(θ+λ) ![]() ,
,
1< ![]() +
+ ![]() sin(θ+λ)<
sin(θ+λ)< ![]() ,
,
∴α+β的取值范围是(1, ![]() )
)
所以答案是: ![]()


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2 ![]() .
. 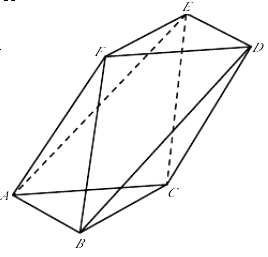
(1)求证:平面ABC⊥平面ACDF;
(2)求平面AEF与平面ACE所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上.过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是公差大于0的等差数列,Sn为数列{an}的前n项和,已知S3=9,且2a1 , a3﹣1,a4+1构成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() =2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.
=2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是关于公差d>0的等差数列{an}的四个命题:p1:数列{an}是递增数列;p2:数列{an}的前n项和Sn是递增数列;p3:数列{ ![]() }是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为( )
}是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为( )
A.p1 , p2
B.p3 , p4
C.p2 , p3
D.p1 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+x2+(a﹣1)x﹣a,(a∈R),当x≥1时,f(x)≥0恒成立.
(1)求实数a的取值范围;
(2)若正实数x1、x2(x1≠x2)满足f(x1)+f(x2)=0,证明:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图: 
(1)某同学不小心把茎叶图中的一个数字弄污了,看不清了,在如图所示的茎叶图中用m表示,若甲运动员成绩的中位数是33,求m的值;
(2)估计乙运动员在这次季后赛比赛中得分落在[20,40]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种, 方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(Ⅰ)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com