练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图所示，在正三棱柱ABC－A1B1C1中，AB＝3，AA1＝4，M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为，设这条最短路线与CC1的交点为N．求：

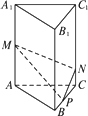
    (1)该三棱柱的侧面展开图的对角线长；

    (2)PC和NC的长．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

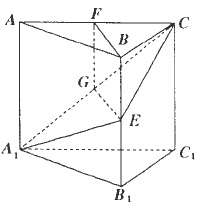
    如下图所示，在正三棱柱ABC－A1B1C1中，E∈BB1，截面A1EC⊥侧面AC1

    (1)求证：BE＝EB1；

    (2)若AA1＝A1B1，求平面A1EC与平面A1B1C1所成的锐二面角的度数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

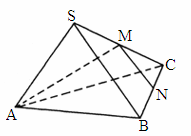
    (汕头联考模拟)如下图所示，在正三棱锥S－ABC中(底面是正多边形，顶点在底面上的射影是底面的中心的棱锥为正棱锥)，M、N分别是棱SC，BC的中点，且MN⊥AM，若侧棱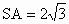，则此正三棱锥S—ABC外接球的表面积是

    [　　]

    A．45π

    B．32π

    C．12π

    D．36π

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

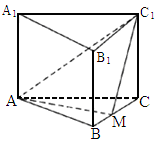
    (唐山一中模拟)如下图所示，正三棱柱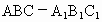的底面边长为a，点M在BC上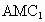，△是以点M为直角顶点的等腰直角三角形．

    (1)求证：点M为边BC的中点；

    (2)求点C到平面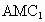的距离；

    (3)求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源：湖南省长沙县实验中学2010届高三第一次月考理科数学试卷 题型：044

    已知三棱柱ABC－A1B1C1三视图如下图所示，其中俯视图是等腰直角三角形，正、侧视图都是正方形，D、E分别为棱CC1和B1C1的中点．

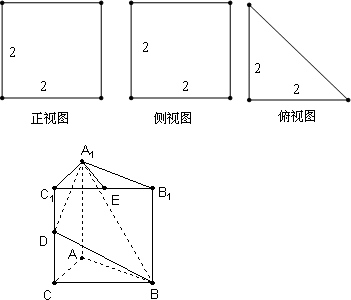
    (1)求异面直线BD与A1E所成角的余弦值；

    (2)在棱AC上是否存在一点F，使EF⊥平面A1BD，若存在，确定点F的位置；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案