
分析 (1)利用同角三角函数和平方关系:sin2α+cos2α=1进行化简;
(2)利用诱导公式进行化简.
解答 解:(1)sin4α+tan2α•cos4α+cos2α
=sin4α+$\frac{si{n}^{2}α}{co{s}^{2}α}$•cos4α+cos2α
=sin2α(sin2α+cos2α)+cos2α
=sin2α+cos2α
=1
(2)$\frac{cos(180°+α)•sin(α+360°)}{sin(-α-180°)•cos(-180°-α)}$
=$\frac{-cosα•sinα}{sinα•(-cosα)}$
=1.
点评 本题考查了三角函数中的恒等变换应用和运用诱导公式化简求值,熟记公式即可解答该题,属于基础题.


科目:高中数学 来源: 题型:解答题
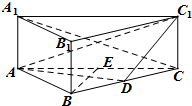 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,AB=BC=2AA1,∠ABC=90°,D是BC的中点,E是AC的中点
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,AB=BC=2AA1,∠ABC=90°,D是BC的中点,E是AC的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{π}{6})<f(\frac{5}{6}π)$ | B. | $\sqrt{3}f(\frac{π}{6})>f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{2})>2f(\frac{π}{3})$ | D. | $2f(\frac{π}{6})<f(\frac{π}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+b2<c2 | B. | $\overrightarrow{AB}$•$\overrightarrow{AC}$<0 | C. | tanAtanB>1 | D. | $\overrightarrow{BC}$•$\overrightarrow{AB}$>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com