
(本题满分12分)
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位: )为
)为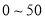 时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为
时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为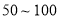 时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为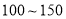 时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为
时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为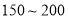 时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为
时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为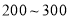 时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为
时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为 以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省
以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省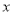 个监测点数据统计如下:
个监测点数据统计如下:
空气污染指数 (单位: |
|
|
|
|
监测点个数 | 15 | 40 |
| 10 |

(Ⅰ)根据所给统计表和频率分布直方图中的信息求出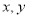 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(Ⅱ)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
(1)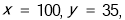 (2)
(2)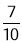 ,
,
【解析】
试题分析:先根据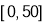 的频数为15,再看分布直方图中频率/组距为0.003,计算出样本容量为x=100,从而求出y,再分别计算每组的频率及频率/组距,画出频率分布直方图;第二步设三个轻度污染点为1,2,3;两个为良的监测点为4,5;从中任意取出2个,用列举法列出所有基本事件共有10种,‘至少右一个为良’的事件有7种,利用概率公式求出即可;
的频数为15,再看分布直方图中频率/组距为0.003,计算出样本容量为x=100,从而求出y,再分别计算每组的频率及频率/组距,画出频率分布直方图;第二步设三个轻度污染点为1,2,3;两个为良的监测点为4,5;从中任意取出2个,用列举法列出所有基本事件共有10种,‘至少右一个为良’的事件有7种,利用概率公式求出即可;
试题解析:(Ⅰ)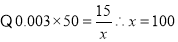 ,
,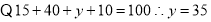
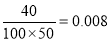 ,
, ,
, 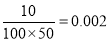 ,根据以上数值画出频率分布直方图如下:
,根据以上数值画出频率分布直方图如下:

(Ⅱ)设A市空气质量状况属于轻度污染3个监测点为1,2,3, 空气质量状况属于良的2个监测点为4,5,从中任取2个的基本事件分别为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种, 其中事件A“其中至少有一个为良”包含的 基本事件为(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,5)共7种,所以事件A“其中至少有一个为良”发生的概率是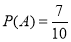 .
.
考点:频率分布直方图和古典概型;


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源:2014-2015学年福建省等高三上学期三校联考理科数学试卷(解析版) 题型:解答题
已知函数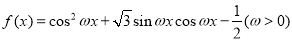 的最小正周期为
的最小正周期为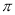 .
.
(I)求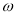 值及
值及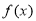 的单调递增区间;
的单调递增区间;
(II)在△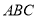 中,
中,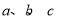 分别是三个内角
分别是三个内角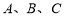 所对边,若
所对边,若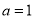 ,
,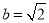 ,
,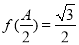 ,求
,求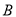 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2015年东北三省四市教研联合体高考模拟试卷(一)理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系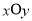 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 的左、右焦点.
的左、右焦点.
(1)以坐标原点为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;
的极坐标方程;
(2)设(1)中直线 与圆锥曲线
与圆锥曲线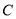 交于
交于 两点,求
两点,求 .
.
查看答案和解析>>
科目:高中数学 来源:2015年东北三省三校高三第一次联合模拟考试文科数学试卷(解析版) 题型:解答题
(本题满分10分)选修4-4: 坐标系与参数方程
已知曲线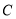 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线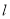 的参数方程是
的参数方程是 (
(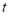 为参数).
为参数).
(Ⅰ)求曲线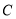 的直角坐标方程和直线
的直角坐标方程和直线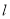 的普通方程;
的普通方程;
(Ⅱ)设点
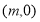 ,若直线
,若直线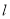 与曲线
与曲线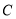 交于
交于 两点,且
两点,且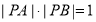 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com