
空间四点最多可确定平面的个数是( )
A. | B. | C. | D. |
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:单选题
正四面体ABCD,线段AB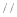 平面
平面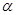 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,则线段AB与EF在平面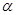 上的射影所成角余弦值的范围是( )
上的射影所成角余弦值的范围是( )
A.[0,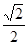 ] ] | B.[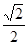 ,1] ,1] | C.[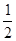 ,1] ,1] | D.[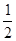 , ,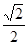 ] ] |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知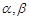 是两个不同的平面,下列四个条件中能推出
是两个不同的平面,下列四个条件中能推出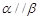 的是( )
的是( )
①存在一条直线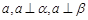 ;
;
②存在一个平面 ;
;
③存在两条平行直线 ;
;
④存在两条异面直线 .
.
| A.①③ | B.②④ | C.①④ | D.②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知命题“如果x⊥y,y∥z,则x⊥z”是假命题,那么字母x,y,z在空间所表示的几何图形可能是( )
| A.全是直线 | B.全是平面 |
| C.x,z是直线,y是平面 | D.x,y是平面,z是直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com