
甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每一小时可获得的利润是100(5x+1﹣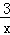 )元.
)元.
(1)求证:生产a千克该产品所获得的利润为100a(5+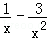 )元;
)元;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
(1)见解析(2)甲厂应以6千克/小时的速度生产,可获得最大利润457500元
【解析】
试题分析:1)生产a千克该产品所用的时间是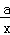 小时,
小时,
∵每一小时可获得的利润是100(5x+1﹣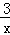 )元,∴获得的利润为100(5x+1﹣
)元,∴获得的利润为100(5x+1﹣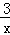 )×
)×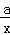 元.
元.
因此生产a千克该产品所获得的利润为100a(5+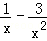 )元.
)元.
(2)生产900千克该产品获得的利润为90000(5+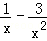 ),1≤x≤10.
),1≤x≤10.
设f(x)=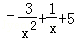 ,1≤x≤10.
,1≤x≤10.
则f(x)=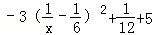 ,当且仅当x=6取得最大值.
,当且仅当x=6取得最大值.
故获得最大利润为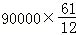 =457500元.
=457500元.
考点:函数模型的选择与应用;二次函数在闭区间上的最值
点评:正确理解题意和熟练掌握二次函数的单调性是解题的关键


科目:高中数学 来源: 题型:
| 3 |
| x |
| 1 |
| x |
| 3 |
| x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是100![]() 元.
元.
(1)求证:生产a千克该产品所获得的利润为100a![]() 元;
元;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试理科数学(上海卷解析版) 题型:解答题
甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求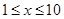 ),每小时可获得利润是
),每小时可获得利润是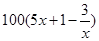 元.
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com