考点:利用导数研究函数的极值
专题:导数的综合应用
分析:利用导数判定函数的单调性,求函数的极值即可,注意对a的讨论.
解答:
解:f′(x)=1-ax-
=
(x∈(-1,+∞)…(2分)
(1)当a=0时,f′(x)=
∴f(x)在(-1,0)上递减,(0,+∞)上递增
∴f(x)的极小值点为0,无极大值点 …(4分)
(2)当a<0时,f′(x)=
∵
=
-1<-1,
∴f(x)在(-1,0)上递减,(0,+∞)上递增,
∴f(x)的极小值点为0,无极大值点.…(6分)
(3)当0<a<1时,f′(x)=
∵
>0,
∴f(x)在(-1,0)上递减,(0,
)上递增,(
,+∞)上递减,
∴f(x)的极小值点为0,极大值点为
,…(8分)
(4)当a>1时,f′(x)=
∵
=
-1∈(-1,0),
∴f(x)在(-1,
)上递减,(
,+∞)上递增,(0,+∞)上递减,
∴f(x)的极小值点为
,极大值点为0.…(10分)
综上:当a≤0时,f(x)的极小值点为0,无极大值点;
当0<a<1时,f(x)的极小值点为0,极大值点为
;
当a>1时,f(x)的极小值点为
,极大值点为0.…(12分)
点评:本题主要考查利用导数研究函数的单调性及极值等知识,考查学生分类讨论思想的运用能力及运算求解能力,属于中档题.



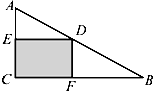 在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.
在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.