
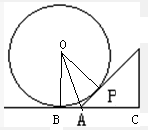
 (2006•丰台区二模)如图,水平地面上有一个大球,现有如下方法测量球的大小:用一个锐角为45°的三角板,斜边紧靠球面,一条直角边紧靠地面,并使三角板与地面垂直,P为三角板与球的切点,如果测得PA=2,则球的表面积为
(2006•丰台区二模)如图,水平地面上有一个大球,现有如下方法测量球的大小:用一个锐角为45°的三角板,斜边紧靠球面,一条直角边紧靠地面,并使三角板与地面垂直,P为三角板与球的切点,如果测得PA=2,则球的表面积为| 2 |
| 2 |
| 1 |
| 2 |
| PA |
| tan22.5° |
| 2 |
| 2 |
| 1 |
| 2 |
| PA |
| OP |
| PA |
| tan22.5° |
| 2 | ||
|
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com