
| A. | sin$\frac{π}{5}$ | B. | cos$\frac{π}{5}$ | C. | -sin$\frac{π}{5}$ | D. | -cos$\frac{π}{5}$ |
分析 根据题意,由同角三角函数的基本关系式可得$\sqrt{1-co{s}^{2}\frac{π}{5}}$=|sin$\frac{π}{5}$|,分析sin$\frac{π}{5}$的符号即可得答案.
解答 解:根据题意,
$\sqrt{1-co{s}^{2}\frac{π}{5}}$=|sin$\frac{π}{5}$|,
而0<$\frac{π}{5}$<$\frac{π}{2}$,sin$\frac{π}{5}$>0,
则$\sqrt{1-co{s}^{2}\frac{π}{5}}$=sin$\frac{π}{5}$,
故选:A.
点评 本题考查同角三角函数的基本关系,注意判断sin$\frac{π}{5}$的符号.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
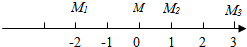 三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)
三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
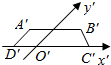 (1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.
(1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com