
分析 将圆C的方程整理为标准形式,找出圆心C的坐标与半径r,根据圆心C到直线y=kx+2的距离不大于圆的直径,利用点到直线的距离公式列出关于k的不等式求出不等式的解集即可得到k的范围.
解答 解:将圆C的方程整理为标准方程得:(x-2)2+(y+1)2=1,
∴圆心C(2,-1),半径r=1,
∵圆心C到直线y=kx+2的距离不大于圆的直径,
∴$\frac{|2k+3|}{\sqrt{{k}^{2}+1}}$≤2,
∴k≤$\frac{9}{2}$.
故答案为:k≤$\frac{9}{2}$.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | sin$\frac{π}{5}$ | B. | cos$\frac{π}{5}$ | C. | -sin$\frac{π}{5}$ | D. | -cos$\frac{π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北石家庄一中高一下期末数学(文)试卷(解析版) 题型:解答题
如图, 是圆
是圆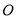 的直径,点
的直径,点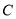 是圆
是圆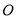 上异于
上异于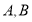 的点,
的点,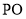 垂直于圆
垂直于圆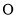 所在的平面,且
所在的平面,且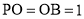 .
.
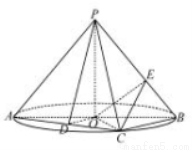
(Ⅰ)若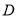 为线段
为线段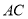 的中点,求证
的中点,求证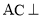 平面
平面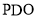 ;
;
(Ⅱ)求三棱锥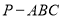 体积的最大值;
体积的最大值;
(Ⅲ)若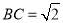 ,点
,点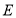 在线段
在线段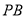 上,求
上,求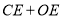 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com