
分析 (1)利用等比中项建立等式关系,消去其中一个未知数,构造二次函数求解.
(2)利用导函数求解.
(3)把$\frac{1}{2|a|}=\frac{a+b}{4|a|}$,分离后,利用基本不等式的性质即可.
解答 解:(1)由题意:x>0,y>0,$\sqrt{2}$是2x与4y的等比中项,则有:2x•4y=2⇒x+2y=1
那么:x2+2y2=(1-2y)2+2y2=6y2-4y+1=$6(y-\frac{1}{3})^{2}+\frac{1}{3}$,当y=$\frac{1}{3}$时,x2+2y2取得最小值为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$
(2)m,n>0,m+n=1,那么:n=1-m(0<m<1).
则:$\frac{{m}^{2}}{m+2}$+$\frac{{n}^{2}}{n+1}$=$\frac{{m}^{2}}{m+2}+\frac{(1-m)^{2}}{2-m}$=$\frac{4}{m+2}+\frac{1}{2-m}-2$
令f(m)=$\frac{{m}^{2}}{m+2}+\frac{(1-m)^{2}}{2-m}$,那么f′(m)=$\frac{(6-m)(3m-2)}{({m}^{2}-4)^{2}}$
令f′(m)=0,解得m=$\frac{2}{3}$.
当0<m<$\frac{2}{3}$时,有f′(m)<0,
当$\frac{2}{3}$<m<1时,有f′(m)>0,
故当m=$\frac{2}{3}$时,f(m)取得极小值,即最小值.
∴f($\frac{2}{3}$)=$\frac{4}{\frac{2}{3}+2}+\frac{1}{2-\frac{2}{3}}-2=\frac{1}{4}$
故最小值为$\frac{1}{4}$.
(3)∵b>0,a+b=2,∴$\frac{1}{2|a|}=\frac{a+b}{4|a|}$,
那么:$\frac{1}{2|a|}+\frac{|a|}{b}$=$\frac{a+b}{4|a|}+\frac{|a|}{b}$
当a>0时,$\frac{a+b}{4|a|}+\frac{|a|}{b}$=$\frac{1}{4}$+$\frac{a}{b}+\frac{b}{4a}≥1$+$\frac{1}{4}$=$\frac{5}{4}$,当且仅当2a=b=$\frac{4}{3}$时取等号.
当a<0时,$\frac{a+b}{4|a|}+\frac{|a|}{b}$=-$\frac{1}{4}$+$\frac{a}{b}+\frac{b}{4a}≥1$-$\frac{1}{4}$=$\frac{3}{4}$,当且仅当a=-2,b=4时取等号.
故答案为$\frac{3}{4}$.
(4)①化为二次函数问题来解决;②利用基本不等式的性质;③利用导函数来求最值.
点评 本题考查了基本不等式的性质的变形与运用欲二次函数相结合求最值的问题.比较综合性.属于中档题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若b7≤a6,则b4+b10≥a3+a9 | B. | 若b7≤a6,则b4+b10≤a3+a9 | ||
| C. | 若b6≥a7,则b3+b9≥a4+a10 | D. | 若b6≤a7,则b3+b9≤a4+a10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
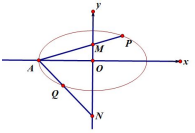 在平面直角坐标系 xOy 中,离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,且A到右准线的距离为6,点P、Q是椭圆C上的两个动点.
在平面直角坐标系 xOy 中,离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,且A到右准线的距离为6,点P、Q是椭圆C上的两个动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | B. | f(x)在$[{\frac{π}{6},\frac{2π}{3}}]$上是减函数 | ||
| C. | f(x)的一个对称中心是$({\frac{5π}{12},0})$ | D. | f(x)的图象的一条对称轴是x=$\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9×10 n-1个 | B. | 9×10 n个 | C. | 9×10 n+1个 | D. | 9×10 n+2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com