练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f（x）=1-xsinx在x=x0处取极值，则（1+x02）（1+cos2x0）=________．

    2
    分析：先根据函数f（x）=1-xsinx在x=x0处取得极值可得出x02=tan2x0，代入（x02+1）（cos2x0+1）化简求值即可得到所求答案
    解答：f（x）=1-xsinx则f′（x）=-sinx-xcosx，
    令-sinx-xcosx=0，
    化得tanx=-x，
    ∴x02=tan2x0，
    ∴（1+x02）（1+cos2x0）
    =（tan2x0+1）（cos2x0+1）
    =
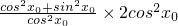
    =2
    故答案为2
    点评：本题主要考查了函数在某点取得极值的条件，解题的关键得出x02=tan2x，从而把求值的问题转化到三角函数中，得以顺利解题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f（x）=|1-
    1x
    |（x＞0），证明：当0＜a＜b，且f（a）=f（b）时，ab＞1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=
    1-
    		1-x
    x
    (x＜0)
    a+x2(x≥0)
    ，要使f（x）在（-∞，+∞）内连续，则a=
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=
    1             (x≤
    		3
    )
    		4-x2
    (
    		3
    ＜x＜2)
    0              (x≥2)
    ，则
    ∫
    2010
    -1
    f（x）dx的值为
    π
    3
    +
    2+
    		3
    2
    π
    3
    +
    2+
    		3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=
    1-|x-1|，x＜2
    1
    2
    f(x-2)，x≥2
    ，则函数F（x）=xf（x）-1的零点的个数为
    6
    6
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=
    1，x＞0
    0，x=0
    -1，x＜0
    ，g（x）=x2f（x-1），则函数g（x）的递减区间是（　　）

    查看答案和解析>>

    同步练习册答案