
 .(Ⅰ)求p的值;(Ⅱ)求
.(Ⅰ)求p的值;(Ⅱ)求 的数学期望E
的数学期望E 与方差D
与方差D .
. 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:不详 题型:解答题
 位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道
位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道 题中任选一题作答,选甲题答对得
题中任选一题作答,选甲题答对得 分,答错得
分,答错得 分;选乙题答对得
分;选乙题答对得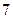 分,答错得
分,答错得 分.若
分.若 位同学的总分为
位同学的总分为 ,求这
,求这 位同学不
位同学不 同得分情况的种数。
同得分情况的种数。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 | 110 | 120 | 125 | 130 | 135 |
| P | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
 | 100 | 115 | 125 | 130 | 145 |
| P | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
 、
、 分别表示A、B两种钢筋的抗拉强度,试比较A、B两种钢筋哪一种质量较好
分别表示A、B两种钢筋的抗拉强度,试比较A、B两种钢筋哪一种质量较好
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. ,求随机变量
,求随机变量 的分布列及数学期望E
的分布列及数学期望E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 城市 | 南宁市 | 柳州市 | 梧州市 | 桂林市 |
| 人数 | 20 | 15 | 5 | 10 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com