
 .
. ,求随机变量
,求随机变量 的分布列及数学期望E
的分布列及数学期望E .
.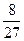 (II)
(II)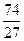
 .
.  可以取0,1,2,3. 当
可以取0,1,2,3. 当 =0时,表示连续5次都没投中,其概率为:
=0时,表示连续5次都没投中,其概率为: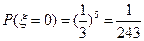 ;当
;当 =1时,表示5次中仅有1次投中,其概率为:
=1时,表示5次中仅有1次投中,其概率为: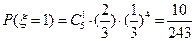 ;当
;当 =2时,表示5次中仅有2次投中,其概率为:
=2时,表示5次中仅有2次投中,其概率为: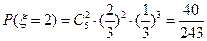 ;当
;当 =3时,表示①连续3次都投中,其概率为:
=3时,表示①连续3次都投中,其概率为: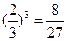 , 或②前3次中有2次投中,且第四次投中,其概率为:
, 或②前3次中有2次投中,且第四次投中,其概率为: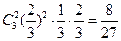 ,
,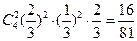 , 即
, 即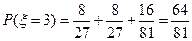 .∴随机变量
.∴随机变量 的概率分布列为:
的概率分布列为: | 0 | 1 | 2 | 3 |
| P | 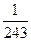 | 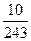 | 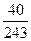 | 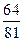 |
 =0×
=0×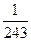 +1×
+1×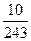 +2×
+2×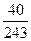 +3×
+3×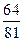 =
=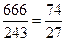 .
. 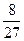 ;(II)甲投篮投中的次数的数学期望是
;(II)甲投篮投中的次数的数学期望是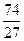 .
. 

科目:高中数学 来源:不详 题型:解答题
 表示所选3人中的女生人数。写出
表示所选3人中的女生人数。写出 的分布列并求出
的分布列并求出 的数学期望。
的数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .(Ⅰ)求p的值;(Ⅱ)求
.(Ⅰ)求p的值;(Ⅱ)求 的数学期望E
的数学期望E 与方差D
与方差D .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (各单位是否录用他相互独立,允许小明被多个单位同时录用) (1)求小明没有被录用的概率;(2)设录用小明的单位个数为
(各单位是否录用他相互独立,允许小明被多个单位同时录用) (1)求小明没有被录用的概率;(2)设录用小明的单位个数为 ,求
,求 的分布列和它的数学期望。
的分布列和它的数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、2
、2 、3
、3 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根. 的分布列及
的分布列及 ;
; 的取值从小到大依次为
的取值从小到大依次为 数列
数列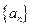 是首项为1,公差为
是首项为1,公差为 的等差数列,设
的等差数列,设 ,当
,当 时,求
时,求 的值。
的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,中国乒乓球女队获得每枚金牌的概率均为
,中国乒乓球女队获得每枚金牌的概率均为 .
. ,按此估计
,按此估计 的分布列和数学期望
的分布列和数学期望 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com