
 的焦点分别为F1(-1,0)、F2(1,0),右准线l交x轴于点A,且
的焦点分别为F1(-1,0)、F2(1,0),右准线l交x轴于点A,且 .
.
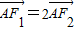 求得a,进而求得b,则椭圆方程可得.
求得a,进而求得b,则椭圆方程可得.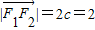 ,∴A(a2,0),
,∴A(a2,0),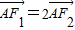 ∴F2为AF1的中点
∴F2为AF1的中点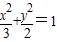 .
.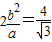 ,
,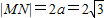 ,四边形DMEN的面积为
,四边形DMEN的面积为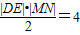 .
.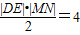 .
.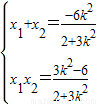
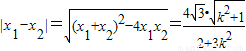 ,
,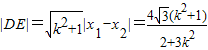 ,
,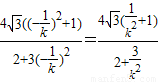 .
.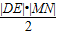 =
=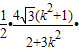
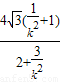 =
=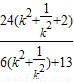 ,
, ,得
,得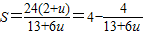
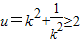 ,
,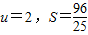 ,且S是以u为自变量的增函数,
,且S是以u为自变量的增函数,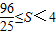 .
.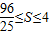 .即四边形DMEN面积的最大值为4,最小值为
.即四边形DMEN面积的最大值为4,最小值为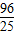 .
.

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
 如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:
如图,抛物线C1:y2=4x的焦点到准线的距离与椭圆C2:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| α 2 |
| y 2 |
| α2-1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广西桂林市、崇左市、防城港市高考第一次联合模拟理科数学试卷(解析版) 题型:解答题
如图,已知椭圆C: +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF ⊥F
⊥F F
F ,O是坐标原点,OB垂直AF
,O是坐标原点,OB垂直AF 于B,且OF
于B,且OF =3OB.
=3OB.

(Ⅰ)求椭圆C的离心率;
(Ⅱ)求t∈(0,b),使得命题“设圆x +y
+y =t
=t 上任意点M(x
上任意点M(x ,y
,y )处的切线交椭圆C于Q
)处的切线交椭圆C于Q 、Q
、Q 两点,那么OQ
两点,那么OQ ⊥OQ
⊥OQ ”成立.
”成立.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省等三校高三2月月考数学理卷 题型:解答题
(本题满分14分)
已知椭圆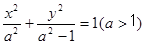 的左右焦点为
的左右焦点为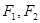 ,抛物线C:
,抛物线C: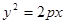 以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
(Ⅰ)求抛物线C的方程和点M的坐标;
(Ⅱ)过F2作抛物线C的两条互相垂直的弦AB、DE,设弦AB、DE的中点分别为F、N,求证直线FN恒过定点;
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(江西) 题型:选择题
设椭圆 的离心率为e=
的离心率为e= ,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)
,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)
A.必在圆x2+y2=2内 B.必在圆x2+y2=2上
C.必在圆x2+y2=2外 D.以上三种情形都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com