
分析 (1)若四位数中不含0,则需要从1,2,3,4,5,6,7这7个数字中任选4个不同的数字组成四位数,利用排列知识,可得结论;
(2)四位数中,是奇数的,末尾是1,3,5,7中的一个,首位是除0与末尾奇数中的一个,利用排列组合知识,可得结论;
(3)首位是5,6,7中的一个,共有C31C61A62=540个,首位是4,千位是5,6,7中的一个,共,有C31A62=90个,首位是4,千位是3,十位是8,有5个,即可得出结论.
解答 解:(1)若四位数中不含0,则需要从1,2,3,4,5,6,7这7个数字中任选4个不同的数字组成四位数,这样的四位数共有A74=840个;
(2)四位数中,是奇数的,末尾是1,3,5,7中的一个,首位是除0与末尾奇数中的一个,故有C41C61A62=720个;
(3)首位是5,6,7中的一个,共有C31C61A62=540个,
首位是4,千位是5,6,7中的一个,共,有C31A62=90个,
首位是4,千位是3,十位是8,有5个,
所以四位数中比4376大的数有540+90+5=635个.
点评 本题考查排列组合知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 19 | C. | 20 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
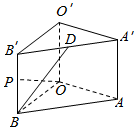 如图所示,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的正切值.
如图所示,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的正切值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com