
其中第(1)(2)问文理科学生都要做,第(3)问按题目要求分文理来做。
已知 为坐标原点,向量
为坐标原点,向量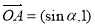 ,
,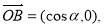
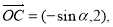 点
点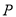 是直线
是直线 上的一点,且
上的一点,且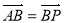 .
.
求点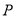 的坐标(用
的坐标(用 表示);
表示);
若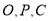 三点共线,求以线段
三点共线,求以线段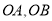 为邻边的平行四边形的对角线长;
为邻边的平行四边形的对角线长;
(3)(文科生做)记函数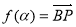 •
•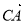 ,且
,且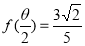 ,求
,求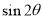 的值.
的值.
(3)(理科生做)记函数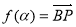 •
•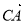 ,
,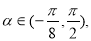 讨论函数
讨论函数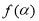 的单调性,并求其值域.
的单调性,并求其值域.
(1)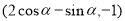 ;(2)
;(2) ;(3)(文)
;(3)(文)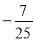 (理)
(理)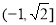 .
.
【解析】
试题分析:
解题思路:(1)利用向量的坐标运算和向量相等进行求解;(2)将三点共线转化为向量共线,再利用共线条件确定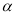 值,利用平行四边形法则与模长公式求解;(3)(文)先根据数量积公式得出
值,利用平行四边形法则与模长公式求解;(3)(文)先根据数量积公式得出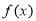 ,再求有关
,再求有关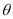 个三角函数值,再利用恒等变形求解;(理)先根据数量积公式得出
个三角函数值,再利用恒等变形求解;(理)先根据数量积公式得出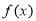 ,再利用
,再利用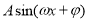 的图像与性质求解.
的图像与性质求解.
规律总结:1.涉及平面向量运算问题,主要思路是:首先,利用平面向量基本定理,选择合适的向量作为基底,来表示有关向量;再利用数量积的有关公式进行求解(模长公式、夹角公式等);
2.涉及三角函数的最值或求值问题,往往先根据三角函数恒等变形化为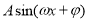 的形式,再利用三角函数的图像与性质进行求解.
的形式,再利用三角函数的图像与性质进行求解.
试题解析:(1)设点 的坐标为
的坐标为 ,则
,则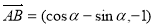 ,
,
∵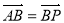 ,∴
,∴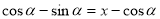 ,
,
∴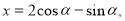

∴点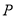 的坐标为
的坐标为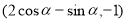
由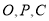 三点共线知:
三点共线知: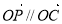 ,
,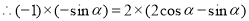 ,
,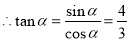
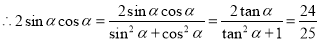
 =
=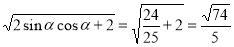
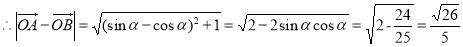
所以以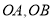 为邻边的平行四边形的对角线长分别为
为邻边的平行四边形的对角线长分别为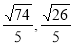
(3)(文科生做)∵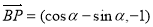 ,
,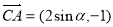
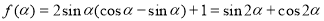 =
=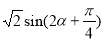
又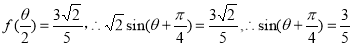
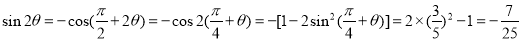
(3)(理科生做)∵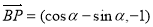 ,
,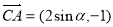
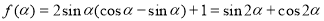 =
=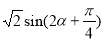
∵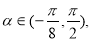 ∴
∴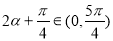 ,
,
∴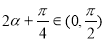 ,即
,即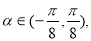 函数
函数 单调递增;
单调递增;
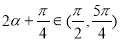 ,即
,即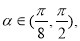 函数
函数 单调递减.
单调递减.
且 ,
,
∴ 的值域为
的值域为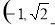 .
.
考点:1平面向量的坐标运算;2.三角函数的图像与性质.


科目:高中数学 来源:2016届广东省顺德市高一上学期第2段考数学试卷(解析版) 题型:选择题
下列所给4个图象中,与所给3件事吻合最好的顺序为( )
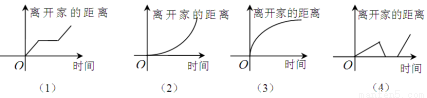
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
A、(1)(2)(4) B、(4)(2)(3) C、(4)(1)(3) D、(4)(1)(2)
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一下学期期中考试文科数学试卷(解析版) 题型:填空题
使函数f(x)=sin(2x+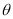 )+
)+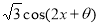 是奇函数,且在[0,
是奇函数,且在[0, ]上是减函数的
]上是减函数的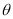 的一个值____________.
的一个值____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com