
 成立;
成立; -1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
-1=S2n-Sn+1恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。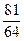 及等差数列an=
及等差数列an=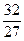 n-
n-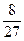 使其满足题意
使其满足题意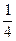 pq(a1+ap)(a1+aq)
pq(a1+ap)(a1+aq)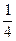 pq[a
pq[a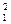 +a1(ap+aq)+apaq]
+a1(ap+aq)+apaq]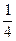 pq(a
pq(a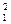 +2a1am+apaq)<
+2a1am+apaq)<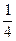 (
(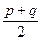 )2[a
)2[a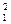 +2a1am+(
+2a1am+(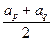 )2]
)2]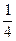 m2(a
m2(a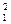 +2a1am+a
+2a1am+a )=[
)=[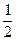 m(a1+am)]2
m(a1+am)]2 ………………………………………………………………………8分
………………………………………………………………………8分 -1=kp2n2+2kpqn+kq2-1
-1=kp2n2+2kpqn+kq2-1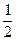 p(n+1)2+
p(n+1)2+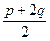 (n+1)
(n+1)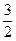 pn2+
pn2+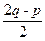 n-(p+q),
n-(p+q),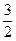 pn2+
pn2+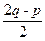 n-(p+q)对一切正整数n成立,
n-(p+q)对一切正整数n成立,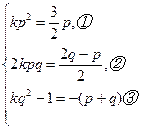
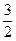 ;
;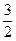 代入②,
代入②,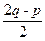 ,q=-
,q=-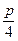 代入③得,
代入③得,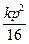 -1=-(p-
-1=-(p-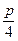 ),将kp=
),将kp=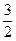 代入得,∴P=
代入得,∴P=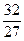 ,
,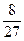 ,k=
,k=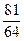
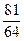 及等差数列an=
及等差数列an=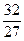 n-
n-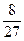 使其满足题意…………………12分
使其满足题意…………………12分

科目:高中数学 来源:不详 题型:解答题
 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且
 (
( 为
为 数列前n项和),求数列通项
数列前n项和),求数列通项 ;
; 满足
满足 ,求证:当
,求证:当 时,恒有
时,恒有 成立.
成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 是数列
是数列 的前
的前 项和,若
项和,若 是非零常数,称数列
是非零常数,称数列 为“和等比数列”。(1)若数列
为“和等比数列”。(1)若数列 是首项为2 ,公比为4的等比数列,则数列
是首项为2 ,公比为4的等比数列,则数列 (填“是”或“不是”) “和等比数列”;
(填“是”或“不是”) “和等比数列”;  是首项为
是首项为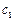 ,公差为
,公差为 的等差数列,且数列
的等差数列,且数列 是“和等比数列”,则
是“和等比数列”,则 与
与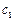 之间满足的关系为
之间满足的关系为 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com