
实数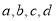 满足
满足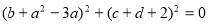 ,则
,则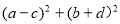 的最小值是 .
的最小值是 .
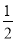 .
.
【解析】
试题分析:由平方数非负,得到: ,且c+d+2=0,由于
,且c+d+2=0,由于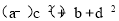 的几何意义:两点A(a,b)、B(c,﹣d)的距离的平方,则为求抛物线
的几何意义:两点A(a,b)、B(c,﹣d)的距离的平方,则为求抛物线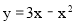 上点A和直线x﹣y+2=0上点B的距离的最小值,先判断直线和抛物线相离,可设直线y=x+t与抛物线相切,由联立抛物线方程,运用判别式为0,求出t,再由两直线的距离公式,即可得到最小值,进而得到答案.
上点A和直线x﹣y+2=0上点B的距离的最小值,先判断直线和抛物线相离,可设直线y=x+t与抛物线相切,由联立抛物线方程,运用判别式为0,求出t,再由两直线的距离公式,即可得到最小值,进而得到答案.
实数a,b,c,d满足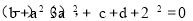
则有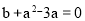 ,且c+d+2=0,
,且c+d+2=0,
由于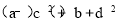 的几何意义:两点A(a,b)、B(c,﹣d)的距离的平方,
的几何意义:两点A(a,b)、B(c,﹣d)的距离的平方,
则为求抛物线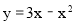 上点A和直线x﹣y+2=0上点B的距离的最小值,
上点A和直线x﹣y+2=0上点B的距离的最小值,
由于联立方程x﹣y+2=0和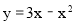 上,消去y,得到
上,消去y,得到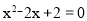 ,方程无实数解,
,方程无实数解,
故直线和抛物线相离,可设直线y=x+t与抛物线相切,
则联立抛物线方程,消去y,得,x2﹣2x+t=0,由判别式为0,即有4﹣4t=0,
即t=1,则切线为:y=x+1,
由于两直线y=x+2与直线y=x+1的距离为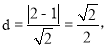 即有抛物线
即有抛物线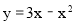 上点A和直线x﹣y+2=0上点B的距离的最小值为
上点A和直线x﹣y+2=0上点B的距离的最小值为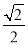 ,则有
,则有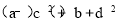 的最小值为
的最小值为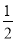 .
.
考点:余弦定理.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年浙江省衢州市五校高三上学期期中联考文科数学试卷(解析版) 题型:解答题
(本题满分15分)已知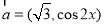 ,
,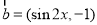 ,
,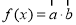
(1)求函数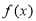 的单调增区间;
的单调增区间;
(2)当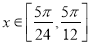 时,求函数
时,求函数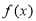 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省衢州市五校高三上学期期中联考理科数学试卷(解析版) 题型:选择题
已知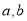 是实数,则“
是实数,则“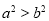 ”是 “
”是 “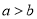 ” 的( )
” 的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高三上学期期中联考理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(Ⅰ)设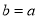 ,若
,若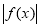 在
在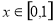 上单调递增,求实数
上单调递增,求实数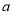 的取值范围;
的取值范围;
(Ⅱ)求证:存在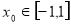 ,使
,使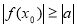 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年豫晋冀高三上学期第二次调研考试文科数学试卷(解析版) 题型:选择题
某校三个年级共有24个班,学校为了了解同学们的心理状况,将每个班编号,依次为l到24,现用系统抽样方法,抽取4个班进行调查,著抽到编号之和为48,则抽到的最小编号为( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试理科数学试卷(解析版) 题型:解答题
已知函数 ,在
,在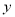 轴上的截距为
轴上的截距为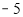 ,在区间
,在区间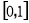 上单调递增,在
上单调递增,在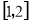 上单调递减,又当
上单调递减,又当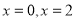 时取得极小值.
时取得极小值.
(1)求函数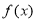 的解析式;
的解析式;
(2)能否找到函数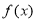 垂直于
垂直于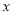 轴的对称轴,并证明你的结论;
轴的对称轴,并证明你的结论;
(3)设使关于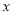 的方程
的方程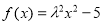 恰有三个不同实根的实数
恰有三个不同实根的实数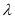 的取值范围为集合
的取值范围为集合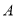 ,且两个非零实根为
,且两个非零实根为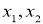 ,试问:是否存在实数
,试问:是否存在实数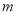 ,使得不等式
,使得不等式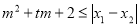 对任意
对任意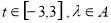 恒成立?若存在,求
恒成立?若存在,求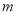 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com