
已知函数 .
.
(Ⅰ)设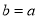 ,若
,若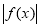 在
在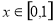 上单调递增,求实数
上单调递增,求实数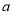 的取值范围;
的取值范围;
(Ⅱ)求证:存在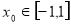 ,使
,使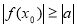 .
.
(Ⅰ)a≥0;(Ⅱ)见解析
【解析】
试题分析:(Ⅰ)分类讨论当a=0时,当a=4时,当a>0,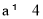 时,当a<0时,判断求解.
时,当a<0时,判断求解.
(Ⅱ)求出|f(1)|=|1+a+b|,|f(﹣1)|=|1﹣a+b|,分类当1+b≥0,a≥0时,
当1+b<0,a<0时,当1+b<0,a<0时,当1+b<0,a>0时,判断大小.
试题解析:函数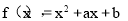
(Ⅰ)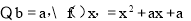
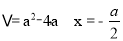 为对称轴,
为对称轴,
①当a=0时,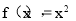
∴|f(x)|在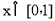 上单调递增,
上单调递增,
∴a=0符合题意,
②当a=4时,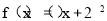 ,
,
∴|f(x)|在x∈[0,1]上单调递增,
∴a=4符合题意,
③当a>0,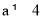 时
时
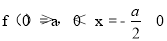 ,
,
∴|f(x)|在x∈[0,1]上单调递增,
∴a>0,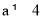 ,符合题意,
,符合题意,
④当a<0时,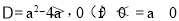 ,
,
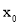 为f(x)=0,的左边的一个零点,
为f(x)=0,的左边的一个零点,
∴|f(x)|在x∈[0,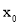 ]上单调递减,
]上单调递减,
∴a<0,不符合题意,
综上a≥0,
(Ⅱ)证明:函数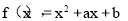
|f(1)|=|1+a+b|,|f(﹣1)|=|1﹣a+b|,
∵当1+b≥0,a≥0时,f(1)=|1+a+b|≥|a|,
当1+b>0,a<0时,|f(﹣1)|=|1﹣a+b|≥|a|,
当1+b<0,a<0时,|f(1)|=|1+a+b|≥|a|,
当1+b<0,a>0时,|f(﹣1)|=|1﹣a+b|≥|a|,
∴存在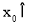 [﹣1,1],使|f(
[﹣1,1],使|f(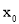 )|≥|a|.
)|≥|a|.
考点:二次函数的性质.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:2014-2015学年福建省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
“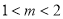 ”是“方程
”是“方程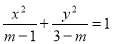 表示的曲线是焦点在
表示的曲线是焦点在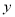 轴上的椭圆”的( )
轴上的椭圆”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高三上学期期中联考文科数学试卷(解析版) 题型:选择题
函数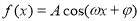 (
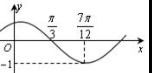
(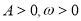 )的图象如右图所示,为了得到
)的图象如右图所示,为了得到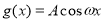 的图象,可以将
的图象,可以将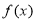 的图象( )
的图象( )
A.向右平移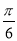 个单位长度
个单位长度
B.向右平移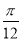 个单位长度
个单位长度
C.向左平移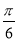 个单位长度
个单位长度
D.向左平移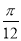 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高三上学期期中联考理科数学试卷(解析版) 题型:选择题
已知函数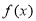 是定义在实数集
是定义在实数集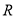 上的不恒为零的偶函数,且对任意实数
上的不恒为零的偶函数,且对任意实数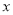 都有
都有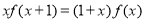 ,则
,则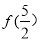 的值是
的值是
A.0 B. C.1 D.
C.1 D.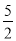
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,输出的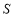 值是 ()
值是 ()
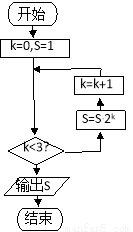
(A)2 (B)4 (C)8 (D)16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com