
分析 (1)利用赋值法,令m=2,n=0,求得f(0)的值,令x<0,且y=-x,则-x>0,f(-x)>1,得到0<f(x)<1,问题得以证明.
(2)利用函数单调性的定义进行证明;
(3)利用函数的单调性化为具体不等式,再分离参数,即可求实数a的取值范围.
解答 (1)证明:①令m=2,n=0,可得f(0+2)=f(0)f(2),∴f(0)=1
②令x<0,且y=-x,则-x>0,f(-x)>1,
∴f(x-x)=f(x)•f(-x)=1,
∵f(-x)>1,
∴0<f(x)<1,
综上所述,f(x)>0在R上恒成立.…(4分)
(2)证明:任取实数x1,x2,∈(-∞,+∞),且x1<x2,
则有x2-x1>0,从而可得0<f(x2-x1)<1
又∵f(x2)=f[x1+(x2-x1)]=f(x1)f(x2-x1)<f(x1)
∴f(x)在R上是减函数…(7分)
(3)令m=n=2可得f(2+2)=f(2)f(2)=$\frac{1}{16}$,
∴f(2)=$\frac{1}{4}$
∴4f(x)f(ax)>f(x2)可化为f(x)f(ax)>f(2)f(x2)
∴f(x+ax)>f(2+x2)
∴x+ax<2+x2,
从而当x>0时,有a+1<$\frac{2+{x}^{2}}{x}$恒成立.
令h(x)=$\frac{2+{x}^{2}}{x}$=x+$\frac{2}{x}$≥2$\sqrt{2}$,从而可得a<2$\sqrt{2}$-1…(12分)
点评 本题主要考查了抽象函数表达式反映函数性质及抽象函数表达式的应用,关键是转化化归的思想的应用,属于中档题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
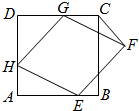 已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.
已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2-i | B. | 1+2i | C. | 2+i | D. | -1+2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com