
 已知:∠BAC=42°,∠CAD=30°,∠BDA=72°,∠BDC=12°,求∠CBD=?(需详细解题过程)
已知:∠BAC=42°,∠CAD=30°,∠BDA=72°,∠BDC=12°,求∠CBD=?(需详细解题过程) 分析 作DE⊥AC于E,CF⊥BD于F,设DE=x,则AD=2x,且∠CDE=24°,求出BD=2x•2cos36°,
CD=$\frac{x}{cos24°}$,CF=$\frac{sin12°}{cos24°}•x$,BF=$\frac{cos12°}{cos24°}$•x,从而BF=BD-DF=4xcos36°-$\frac{cos12°}{cos24°}$x,
由此求出tan∠CBD=tan6°,由此能求出∠CBD.
解答  解:作DE⊥AC于E,CF⊥BD于F,
解:作DE⊥AC于E,CF⊥BD于F,
设DE=x,则AD=2x,且∠CDE=24°,
∴BD=AD•$\frac{sin72°}{sin30°}$=2x•2cos36°,
CD=$\frac{DE}{cos24°}$=$\frac{x}{cos24°}$,
∴CF=CD•sin12°=$\frac{sin12°}{cos24°}•x$,
BF=CD•cos12°=$\frac{cos12°}{cos24°}$•x,
∴BF=BD-DF=4xcos36°-$\frac{cos12°}{cos24°}$x,
∴tan$∠CBD=\frac{CF}{BF}$
=$\frac{\frac{sin12°}{cos24°}•x}{4xcos30°-\frac{cos12°}{cos24°}•x}$
=$\frac{sin12°}{2(cos60°+cos12°)-cos12°}$
=$\frac{sin12°}{1+cos12°}$=$\frac{2sin6°cos6°}{2co{s}^{2}6°}$=tan6°,
∴∠CBD=6°.
点评 本题考角的求法,考查正弦定理、三角函数、正切加法定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:解答题
在一次篮球定点投篮训练中,规定每人最多投 次,在
次,在 处每投进一球得
处每投进一球得 分; 在
分; 在 处每投进一球得
处每投进一球得 分,如果前两次得分之和超过
分,如果前两次得分之和超过 分就停止投篮 ; 否則投第三次 , 某向学在
分就停止投篮 ; 否則投第三次 , 某向学在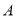 处的投中率,
处的投中率, ,在
,在 处的投中率为
处的投中率为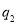 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求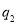 的值;
的值;
(2)求随机变量 的数学期望;
的数学期望;
(3)试比较该同学选择上述方式投篮得分超过 分与选择都在
分与选择都在 处投篮得分超过
处投篮得分超过 分的概率的大小.
分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,BD=$\sqrt{3}$,
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,BD=$\sqrt{3}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<t<3 | B. | 1<t<4 | C. | 2<t<3 | D. | 2<t<4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在定义域是增函数 | B. | f(x)的对称中心是($\frac{kπ}{4}$-$\frac{π}{6}$,0)(k∈Z) | ||
| C. | f(x)是奇函数 | D. | f(x)的对称轴是x=$\frac{kπ}{2}$+$\frac{π}{12}$(k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com