
| A. | 1<t<3 | B. | 1<t<4 | C. | 2<t<3 | D. | 2<t<4 |
分析 易得曲线C:(x-4)2+y2=1.设点P(t,$\sqrt{2}$(t-1)),只需点P到圆心(4,0)的距离小于2+r即可,即(t-4)2+2(t-1)2<(2+1)2,解得t的范围.
解答 解:设M(x,y),∵M满足|OM|=4|AM|,
∴${x}^{2}+{y}^{2}=16[(x-\frac{15}{4})^{2}+{y}^{2}]$化简得:(x-4)2+y2=1
∴曲线C:(x-4)2+y2=1
设点P(t,$\sqrt{2}$(t-1)),只需点P到圆心(4,0)的距离小于2+r即可.
∴(t-4)2+2(t-1)2<(2+1)2.
解得:1<t<3.
故选:A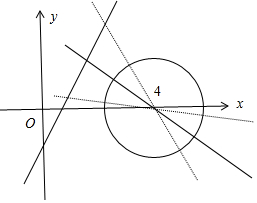
点评 本题考查圆的方程的应用,直线与圆的位置关系,考查分析问题解决问题的能力.属于中档题,


科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:选择题
已知双曲线 的右焦点为
的右焦点为 ,直线
,直线 与双曲线
与双曲线 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为 为坐标原点,若
为坐标原点,若 的面积为
的面积为 ,则双曲线
,则双曲线 的离心率为( )
的离心率为( )
A.  B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠DAB=$\frac{π}{3}$,AD:AB=2:3,BD=$\sqrt{7}$,AB⊥BC.
如图,在四边形ABCD中,∠DAB=$\frac{π}{3}$,AD:AB=2:3,BD=$\sqrt{7}$,AB⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若任意n∈N*总有$\overrightarrow{{c}_{n}}$⊥$\overrightarrow{{b}_{n}}$成立,则数列{an}是等比数列 | |
| B. | 若任意n∈N*总有$\overrightarrow{{c}_{n}}$∥$\overrightarrow{{b}_{n}}$成立,则数列{an}是等比数列 | |
| C. | 若任意n∈N*总有$\overrightarrow{{c}_{n}}$⊥$\overrightarrow{{b}_{n}}$成立,则数列{an}是等差数列 | |
| D. | 若任意n∈N*总有$\overrightarrow{{c}_{n}}$∥$\overrightarrow{{b}_{n}}$成立,则数列{an}是等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{2}$ | B. | $\sqrt{2}+2\sqrt{5}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}+2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5+2$\sqrt{2}$] | B. | (-∞,8] | C. | [$\frac{26}{3}$,+∞) | D. | (-∞,5+2$\sqrt{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com