
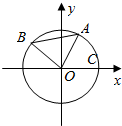
 已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α
已知A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形,记∠AOC=α分析 (1)可得A点纵坐标为$\frac{4}{5}$,由三角函数的定义可得tanα=$\frac{4}{3}$,由诱导公式可得;
(2)由题意可得tan∠COB=-$\frac{3}{4}$,进而可得B(-$\frac{4}{5}$,-$\frac{3}{5}$),由两点之间的距离公式可得.
解答 解:(1)当A点的横坐标为$\frac{3}{5}$时,纵坐标为$\frac{4}{5}$,
∴由三角函数的定义可得tanα=$\frac{4}{3}$,
∴tan(540°-α)=tan(180°×3-α)=-tanα=-$\frac{4}{3}$;
(2)∵tan(α+60°)=tan∠COB=-$\frac{3}{4}$,
∴B(-$\frac{4}{5}$,-$\frac{3}{5}$),又C(1,0),
∴B、C两点之间的距离为$\sqrt{(-\frac{4}{5}-1)^{2}+(-\frac{3}{5}-0)^{2}}$=$\frac{3\sqrt{10}}{25}$
点评 本题考查三角函数的定义,涉及两点间的距离公式,属基础题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为$\frac{8}{{e}^{2}}$ | B. | 最大值为$\frac{4}{{e}^{2}}$ | C. | 最小值为$\frac{8}{{e}^{2}}$ | D. | 最小值为$\frac{4}{{e}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{2}{3}$,$\frac{3}{4}$) | D. | (0,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com