
三个女生和五个男生排成一排.
(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不同的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
(5)如果三个女生站在前排,五个男生站在后排,有多少种不同的排法?
(1) 4320;(2) 14400;(3) 14400;(4) 36000;(5) 720
【解析】
试题分析: (1)(捆绑法)因为三个女生必须在一起,所以可以把她们看成一个整体,这样同五个男生合在一起共有六个元素,排成一排共有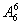 种不同排法.对于其中的每一种排法,三个女生之间又都有
种不同排法.对于其中的每一种排法,三个女生之间又都有 种不同的排法,因此共有
种不同的排法,因此共有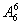 ·
· =4320种不同的排法.
=4320种不同的排法.
(2)(插空法)要保证女生全分开,可先把五个男生排好,每两个相邻的男生之间一个空,这样共有六个位置,再把三个女生插入这六个位置中,使得每个位置至多有一个女生插入,就能保证任意两个女生都不相邻,因此共有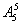 ·
·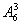 =14400种不同的排法.
=14400种不同的排法.
(3)(位置分析法):因为两端不能排女生,所以两端只能挑选5个男生中的2人,有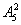 种不同的排法,对于其中的任意一种排法,其余6位都有
种不同的排法,对于其中的任意一种排法,其余6位都有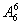 种排法,所以共有
种排法,所以共有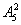 ·
·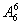 =14400种不同的排法.
=14400种不同的排法.
(4)因为只要求两端不都排女生,所以如果首位排了男生,则末位就不再受条件限制了,这样可以有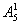 ·
·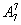 种不同的排法;如果首位是女生,有
种不同的排法;如果首位是女生,有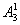 种排法,这时末位就只能排男生,共有
种排法,这时末位就只能排男生,共有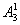 ·
·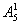 ·
·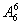 种不同的排法,所以共有
种不同的排法,所以共有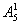 ·
·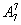 +
+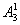 ·
·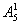 ·
·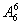 =36000种不同的排法.
=36000种不同的排法.
(5)三个女生站在前排,五个男生站在后排,只需第一步,排女生有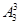 种排法;第二步排男生,有
种排法;第二步排男生,有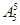 种排法,所以共有
种排法,所以共有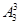
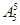 =720种排法。
=720种排法。
考点:主要考查有条件的排列问题解法,考查学生的逻辑思维能力及计算能力。
点评:本题综合考查了有条件的排列问题解法,有“直接法”“间接法”“捆绑法”“插空法”,是一道很好的题目。事实上,将题中“女生”“男生”分别换成其它事物,解法相同。


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
(3)如果两端都不能排女生,可有多少种不同的排法?
(4)如果两端不能都排女生,可有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
(3)如果两端都不能排女生,可有多少种不同的排法?
(4)如果两端不能都排女生,可有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
三个女生和五个男生排成一排,
(1)如果女生必须全排在一起,可有多少种不同的排法?
(2)如果女生必须全分开,可有多少种不同的排法?
(3)如果两端都不能排女生,可有多少种不同的排法?
(4)如果两端不能都排女生,可有多少种不同的排法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com