
分析 (1)换元根据t=2x∈[$\frac{1}{2}$,2],g(t)=t2-t单调递增,即可求f(x)的值域;
(2)配方得出:(2s+2t)2-2•2s+t-(2s+2t)=0,a2-2b-a=0,a≥2$\sqrt{b}$,a≥2$\sqrt{\frac{{a}^{2}-a}{2}}$,a>0,求解即可得出b=$\frac{{a}^{2}-a}{2}$,1<a≤2;
(3)g(x)=$\frac{1}{2}$(x2-x)∈(0,1],f(x)∈[-$\frac{1}{4}$,2],对任意x1∈D,都存在x2∈[-1,1],使得g(x1)=f(x2)+m成立,即可求实数m的取值范围.
解答 解:(1)∵函数f(x)=4x-2x,f(x)的定义域为[-1,1]时,
∴t=2x∈[$\frac{1}{2}$,2],g(t)=t2-t单调递增,
∵g($\frac{1}{2}$)=-$\frac{1}{4}$,g(2)=2,
∴f(x)的值域为:[-$\frac{1}{4}$,2].
(2)∵f(s)+f(t)=0,
∴4s-2s+4t-2t=0,
化简得出:(2s+2t)2-2•2s+t-(2s+2t)=0,
∵a=2s+2t,b=2s+t.2s+2t≥2$\sqrt{{2}^{s+t}}$.a≥2$\sqrt{b}$
∴a2-2b-a=0,a≥2$\sqrt{b}$,a≥2$\sqrt{\frac{{a}^{2}-a}{2}}$,a>0
即b=$\frac{{a}^{2}-a}{2}$,1<a≤2,D=(1,2];
(3)g(x)=$\frac{1}{2}$(x2-x)∈(0,1],f(x)∈[-$\frac{1}{4}$,2].
∵对任意x1∈D,都存在x2∈[-1,1],使得g(x1)=f(x2)+m成立,
∴(0,1]⊆[-$\frac{1}{4}$+m,2+m].
∴-1≤m≤$\frac{1}{4}$.
点评 本题综合考查了函数的性质,配方求解,考查换元法,考查学生分析解决问题的能力,属于综合题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
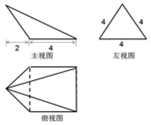
| A. | $\frac{32}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{{64\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形,这个灰色菱形可以分割成n个边长为1的小正三角形.若m:n=47:25,则三角形ABC的边长是( )
如图,将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形,这个灰色菱形可以分割成n个边长为1的小正三角形.若m:n=47:25,则三角形ABC的边长是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
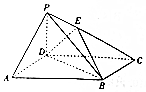 如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com