
 ,
, 是平面上一动点,且满足
是平面上一动点,且满足 ,
, 的轨迹
的轨迹 对应的方程;
对应的方程; 在曲线
在曲线 上,过点
上,过点 作曲线
作曲线 的两条弦
的两条弦 ,且
,且 的斜率为
的斜率为 满足
满足 ,试判断动直线
,试判断动直线 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.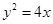 即为
即为 对应的方程;(2)直线
对应的方程;(2)直线 恒过定点
恒过定点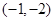 .
. 可知
可知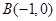 …………………………1分
…………………………1分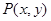 ,则
,则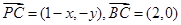 ,
,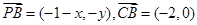 …………2分
…………2分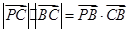 得:
得: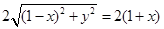
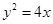 即为
即为 对应的方程, …………………………5分
对应的方程, …………………………5分 代入
代入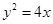 得
得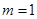 ∴
∴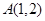 …………………………6分
…………………………6分 的方程为:
的方程为: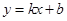
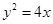 消
消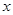 得:
得: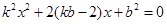 …………………………7分
…………………………7分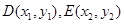
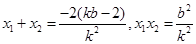 …………………………8分
…………………………8分 ∴
∴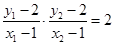 且
且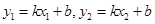
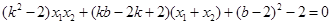
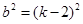
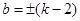 …………………………10分
…………………………10分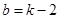 时代入
时代入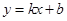 得:
得: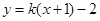 过定点
过定点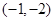
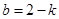 时代入
时代入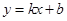 得:
得: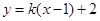 过
过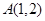 ,不合题意,舍去.
,不合题意,舍去. 恒过定点
恒过定点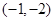 .…………………………12分
.…………………………12分

科目:高中数学 来源:不详 题型:解答题
 上的任意一点到它两个焦点
上的任意一点到它两个焦点 的距离之和为
的距离之和为 ,且它的焦距为2.
,且它的焦距为2. 的方程;
的方程; 与椭圆
与椭圆 交于不同两点
交于不同两点 ,且线段
,且线段 的中点
的中点 不在圆
不在圆 内,求实数
内,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
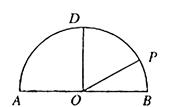
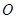 为圆心,
为圆心,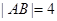 为直径的半圆
为直径的半圆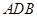 中,
中,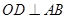 ,
,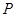 是半圆弧上一点,
是半圆弧上一点,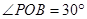 ,曲线
,曲线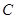 是满足
是满足 为定值的动点
为定值的动点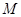 的轨迹,且曲线
的轨迹,且曲线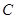 过点
过点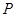 .
.
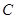 的方程;
的方程;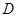 的直线l与曲线
的直线l与曲线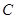 相交于不同的两点
相交于不同的两点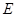 、
、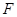
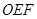 的面积不小于
的面积不小于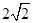 ,求直线
,求直线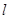 斜率的取值范围.
斜率的取值范围. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
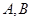 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在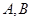 两城市的周边修建城际轻轨,假设
两城市的周边修建城际轻轨,假设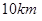 为一个单位距离,
为一个单位距离,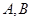 两城市相距
两城市相距 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为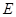 ,使轻轨
,使轻轨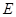 上的点到
上的点到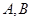 两城市的距离之和为
两城市的距离之和为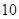 个单位距离,
个单位距离,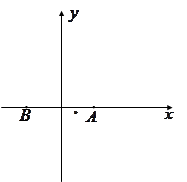
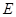 的方程;
的方程;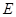 上建一个加油站
上建一个加油站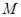 与一个收费站
与一个收费站 ,使
,使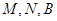 三点在一条直线上,并且
三点在一条直线上,并且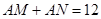 个单位距离,求
个单位距离,求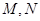 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?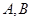 两城市之间有一条与
两城市之间有一条与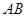 所在直线成
所在直线成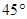 的笔直公路
的笔直公路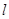 ,直线
,直线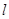 与曲线
与曲线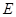 交于
交于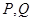 两点,求四边形
两点,求四边形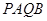 的面积的最大值.
的面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com