将函数
（
）的图象绕坐标原点逆时针旋转
（为锐角），若所得曲线仍是一个函数的图象，则的最大值为（ ）
A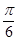． | B． | C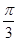． | D． |
阅读快车系列答案科目：高中数学 来源： 题型：单选题
给出以下命题：
①对于平面几何中的命题：“夹在两条平行线之间的平行线段相等”，在立体几何中，类比上述命题，可以得到命题：“夹在两个平行平面间的平行线段相等”．
②
＝2；
③已知函数
的图象与直线
有相异三个公共点，则
的取值范围是(－2,2)
其中正确命题是（ ）
| A．①②③ | B．①② | C．①③ | D．②③ |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
为了得到函数y=2x﹣3﹣1的图象，只需把函数y=2x上所有点（ ）
| A．向右平移3个单位长度，再向下平移1个单位长度 |
| B．向左平移3个单位长度，再向下平移1个单位长度 |
| C．向右平移3个单位长度，再向上平移1个单位长度 |
| D．向左平移3个单位长度，再向上平移1个单位长度 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
下列各组函数中表示同一函数的是（ ）
A．y= 和y= |
B．y=|x|和y= |
| C．y=logax2和y=2logax（a＞0a≠1） |
| D．y=x和y=logaax（a＞0，a≠1） |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，∴k=f'（0）=
=tan30°，可得切线的倾斜角为 30°，因此，要使旋转后的图象仍为一个函数的图象，旋转θ后的切线倾斜角最多为 90°，也就是说，最大旋转角为 90°-30°=60°，即θ的最大值为60°，故答案为：C.
在定义域内的任意实数
及
，都有
及
成立，则称函数
函数”.现给出下列四个函数：
；
.其中是“
的函数
（
）有两个单调区间，则实数
，
，
满足（ ）
且
其中
表示不超过
的最大整数，（如
,
,
）.若直线
与函数
的图象恰有三个不同的交点，则实数
的取值范围是 
的值域为（ ）