
已知函数 (其中
(其中 为常数且
为常数且 )在
)在 处取得极值.
处取得极值.
(I) 当 时,求
时,求 的单调区间;(II) 若
的单调区间;(II) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
(I)因为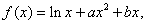 所以
所以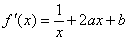 ………………2分
………………2分
因为函数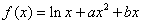 在
在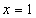 处取得极值
处取得极值
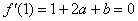 ………………3分
………………3分
当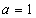 时,
时,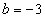 ,
,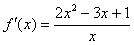 ,
,
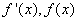 随
随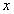 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
|
| 极大值 |
| 极小值 |
|
所以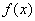 的单调递增区间为
的单调递增区间为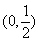 ,
,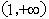 单调递减区间为
单调递减区间为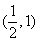 ………………6分
………………6分
(II)因为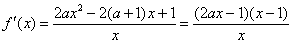
令 ,
,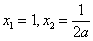 ………………7分
………………7分
因为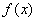 在
在 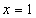 处取得极值,所以
处取得极值,所以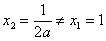
当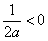 时,
时,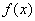 在
在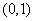 上单调递增,在
上单调递增,在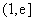 上单调递减
上单调递减
所以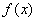 在区间
在区间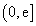 上的最大值为
上的最大值为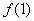 ,令
,令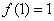 ,解得
,解得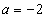 ………………9分
………………9分
当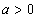 ,
,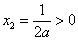
当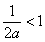 时,
时,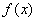 在
在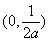 上单调递增,
上单调递增,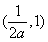 上单调递减,
上单调递减,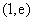 上单调递增
上单调递增
所以最大值1可能在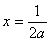 或
或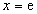 处取得
处取得
而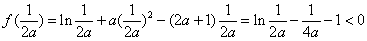
所以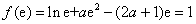 ,解得
,解得 ………………11分
………………11分
当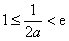 时,
时,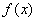 在区间
在区间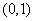 上单调递增,
上单调递增,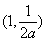 上单调递减,
上单调递减,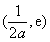 上单调递增
上单调递增
所以最大值1可能在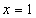 或
或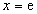 处取得
处取得
而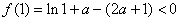 所以
所以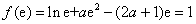 ,
,
解得 ,与
,与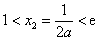 矛盾………………12分
矛盾………………12分
当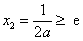 时,
时,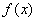 在区间
在区间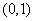 上单调递增,在
上单调递增,在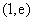 单调递减,
单调递减,
所以最大值1可能在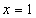 处取得,而
处取得,而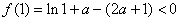 ,矛盾
,矛盾
综上所述,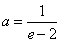 或
或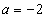


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )
(A)60 (B)480 (C)420 (D)70、
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示是计算函数y= 的值的程序框图,则在①、②、③处应分别填入的是( )
的值的程序框图,则在①、②、③处应分别填入的是( )
 A.y=-x,y=0,y=x2
A.y=-x,y=0,y=x2
B.y=-x,y=x2,y=0
C.y=0,y=x2,y=-x
D.y=0,y=-x,y=x2http://w ww .xkb1. com
查看答案和解析>>
科目:高中数学 来源: 题型:
在一个袋子中装有分别标 注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
A.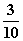 B.
B.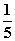 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学推荐甲、乙、丙、丁4名同学参加A、B、C三所大学的自主招生考试.每名同学只推荐一所大学,每所大学至少推荐一名.则不推荐甲同学到A大学的推荐方案有( )
A.18种 B.24种 C.54种 D.60种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com