练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．设集合U={-1，0，1，2，3，4，5}，A={1，2，3}，B={-1，0，1，2}，则A∩（∁UB）=（　　）
    A．{1，2，3}B．{1，2}C．{3}D．{2}

    分析 利用集合的补集的定义求出集合B的补集；再利用集合的交集的定义求出A∩CUB

    解答 解：∵U={-1，0，1，2，3，4，5}，A={1，2，3}，B={-1，0，1，2}，
    ∴∁UB={3，4，5}
    A∩∁UB={1，2，3}∩{3，4，5}={3}
    故选：C．

    点评 本题考查集合的交集、并集、补集的定义并用定义解决简单的集合运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．设$\overrightarrow{a}$、$\overrightarrow{b}$分别是两条异面直线l1、l2的方向向量，向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角的取值范围为A．l1、l2所成的角的取值范围为B，则“a∈A”是“a∈B”的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设函数f（x）=x2e-x，g（x）=xlnx．
    （1）若F（x）=f（x）-g（x），证明：F（x）在（0，+∞）上存在唯一零点；
    （2）设函数h（x）=min{f（x），g（x）}，（min{a，b}表示a，b中的较小值），若h（x）≤λ，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知抛物线C：y2=2px（p＞0）的焦点为F，直线y=4与C的交点为P，与y轴的交点为Q，且|PF|=$\frac{3}{2}$|PQ|，则抛物线C的方程为y2=4$\sqrt{2}$x，点P的坐标为（2$\sqrt{2}$，4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

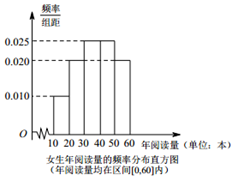    18．每年的4月23日为世界读书日，为调查某高校学生（学生很多）的读书情况，随机抽取了男生，女生各20人组成的一个样本，对他们的年阅读量（单位：本）进行了统计，分析得到了男生年阅读量的频数分布表和女生年阅读量的频率分布直方图．
    男生年阅读量的频数分布表（年阅读量均在区间[0，60]内）
    本/年[0，10）[10，20）[20，30）[30，40）[40，50）[50，60]
    频数318422
    （Ⅰ）根据女生年阅读量的频率分布直方图估计该校女生年阅读量的中位数；
    （Ⅱ）若年不小于40本为阅读丰富，否则为阅读不丰富，依据上述样本研究年阅读量与性别的关系，完成下列2×2列联表，并判断是否有99%的把握认为阅读丰富与性别有关；
    性别　　　 阅读量丰富不丰富合计
    男
    女
    合计
    （Ⅲ）在样本中，从年阅读量在[50，60]的学生中，随机抽取2人参加全市的征文比赛，记这2人中男生人数为ξ，求ξ的分布列和期望．
    附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
    P（K2≥k0）0.0250.0100.005
    k05.0246.6357.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知向量$\overrightarrow{BA}$=（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{BC}$=（$\sqrt{3}$，1），则∠ABC=$\frac{π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知集合A={x∈N|x＜3}，B={x|x=a-b，a∈A，b∈A}，则A∩B=（　　）
    A．{1，2}B．{-2，-1，0，1，2}C．{1}D．{0，1，2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知A是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的右顶点，过左焦点F与y轴平行的直线交双曲线于P，Q两点，若△APQ是锐角三角形，则双曲线C的离心率范围是（　　）
    A．$（{1，\sqrt{2}}）$B．$（{1，\sqrt{3}}）$C．（1，2）D．（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设函数f（x）=（x+b）lnx，y=f（x）的图象在点（1，f（1））处的切线与直线y=3x平行．
    （1）求b的值；
    （2）若函数$g（x）={e^x}（\frac{f（x）}{x+2}-2a）$（a≠0），且g（x）在区间（0，+∞）上是单调函数，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案