
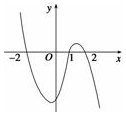
 设函数f(x)在R上可导,其导函数f′(x)且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数f′(x)且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(-2)和极小值f(2) | B. | 函数f(x)有极大值f(-2)和极小值f(1) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(-2) | D. | 函数f(x)有极大值f(2)和极小值f(1) |
分析 结合函数图形,对x分区间讨论f(x)与0大小关系,从而推导出f(x)在区间上的单调性即可;
解答 解:由图形推导可知:
当x<-2时,y>0,1-x>0⇒f'(x)>0,故f(x)在(-∞,-2)上单调递增;
当-2<x<1时:y<0,1-x>0⇒f'(x)<0,故f(x)在(-2,1)上单调递减;
当1<x<2时:y>0,1-x<0⇒f'(x)<0,故f(x)在(1,2)上单调递减;
当x>2时:y<0,1-x<0⇒f'(x)>0,故f(x)在(2,+∞)上单调递增;
故函数f(x)在x=-2时取得极大值,在x=2时取得极小值;
故选:A.
点评 本题主要考查了导函数与原函数图形的关系,以及数学结合与分析推理等知识点,属中等题.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p,¬q都是真命题,则命题“p∧q”为真命题 | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0或y≠0” | |
| C. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| D. | 命题“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com