
 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE.分析 (1)推导出PD⊥BC,BC⊥CD,从而BC⊥平面PCD,进而BC⊥DE,再由DE⊥PC,能证明DE⊥平面PBC.
(2)由BC⊥平面PCD,DE⊥平面PBC,能得到四面体EBCD是一个鳖臑,其四个面的直角分别是∠BCD,∠BCE,∠DEC,∠DEB.
(3)由PD是阳马P-ABCD的高,得到${V}_{1}=\frac{1}{3}{S}_{ABCD}•PD$=$\frac{1}{3}×BC×CD×PD$;由DE是鳖臑D-BCE的高,得到${V}_{2}=\frac{1}{3}{S}_{△BCE}•DE=\frac{1}{6}×BC×CE×DE$.由此能求出$\frac{{V}_{1}}{{V}_{2}}$的值.
解答 证明:(1)因为PD⊥底面ABCD,所以PD⊥BC.…(1分)
由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,
所以BC⊥平面PCD.…(3分)
DE?平面PCD,所以BC⊥DE.…(4分)
又因为PD=CD,点E是PC的中点,所以DE⊥PC. …(5分)
而PC∩BC=C,所以DE⊥平面PBC.…(6分)
解:(2)由BC⊥平面PCD,DE⊥平面PBC,
可知四面体EBCD的四个面都是直角三角形,即四面体EBCD是一个鳖臑,…(7分)
其四个面的直角分别是∠BCD,∠BCE,∠DEC,∠DEB.…(8分)
(3)由已知,PD是阳马P-ABCD的高,
所以${V}_{1}=\frac{1}{3}{S}_{ABCD}•PD$=$\frac{1}{3}×BC×CD×PD$;…(8分)
由(1)知,DE是鳖臑D-BCE的高,BC⊥CE,…(9分)
所以${V}_{2}=\frac{1}{3}{S}_{△BCE}•DE=\frac{1}{6}×BC×CE×DE$.
在Rt△PDC中,因为PD=CD,点E是PC的中点,所以DE=CE+$\frac{\sqrt{2}}{2}CD$,…(10分)
于是 $\frac{{V}_{1}}{{V}_{2}}=\frac{\frac{1}{3}BC•CD•PD}{\frac{1}{6}BC•CE•DE}$=$\frac{2CD•PD}{CE•DE}$=4.…(12分)
点评 本题考查线面垂直的证明,考查四面体EBCD是否为鳖臑的判断,考查两个几何体的比值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1005 | B. | 1006 | C. | 1007 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg(x2+$\frac{1}{4}$)>lg x(x>0) | |
| B. | sin x+$\frac{1}{sinx}$≥2(x≠kπ,k∈Z) | |
| C. | 函数 y=$\frac{x}{{x}^{2}+1}$,x∈(0,$\frac{3}{4}$)的最大值为$\frac{1}{2}$ | |
| D. | x2+1≥2|x|(x∈R) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
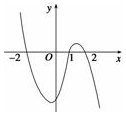 设函数f(x)在R上可导,其导函数f′(x)且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数f′(x)且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(-2)和极小值f(2) | B. | 函数f(x)有极大值f(-2)和极小值f(1) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(-2) | D. | 函数f(x)有极大值f(2)和极小值f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com