
【题目】已知椭圆![]() 与
与![]() 轴负半轴交于
轴负半轴交于![]() ,离心率
,离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与直线
垂直的直线与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的取值范围及
的取值范围及![]() 取得最小值时直线
取得最小值时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 的取值范围是
的取值范围是![]() ,
,![]() 最小值为
最小值为![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
【解析】
(1)根据已知条件得出![]() ,再由离心率可得出
,再由离心率可得出![]() 的值,并求出
的值,并求出![]() 的值,由此可得出所求椭圆的方程;
的值,由此可得出所求椭圆的方程;
(2)由题意可知,直线![]() 与
与![]() 轴不重合,设直线
轴不重合,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,利用弦长公式求出
的方程联立,列出韦达定理,利用弦长公式求出![]() ,并求出点
,并求出点![]() 的坐标,进而求得
的坐标,进而求得![]() ,由此可得出
,由此可得出![]() 的表达式,利用导数求出
的表达式,利用导数求出![]() 的取值范围,以及
的取值范围,以及![]() 取最小值时对应的直线方程.
取最小值时对应的直线方程.
(1)由题有![]() ,
,![]() ,
,![]() ,
,![]() .
.
因此,椭圆方程为![]() ;
;
(2)当直线![]() 与
与![]() 轴重合时,则直线
轴重合时,则直线![]() 的垂线与直线
的垂线与直线![]() 平行,不合乎题意.
平行,不合乎题意.
设![]() ,将其与曲线
,将其与曲线![]() 的方程联立,得
的方程联立,得![]() .
.
即![]() .
.
设![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
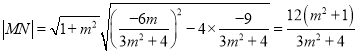 ,
,
将直线![]() 与
与![]() 联立,得
联立,得![]() ,
,
![]() .
.
 .
.
设![]() ,构造
,构造![]() .
.
![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以![]() 的取值范围是
的取值范围是![]() ,
,
当![]() 取得最小值
取得最小值![]() 时,
时,![]() , 此时直线
, 此时直线![]() 的方程为
的方程为 ![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,等腰梯形ABCD中,AB∥CD,AD=AB=BC=1,CD=2,E为CD中点,以AE为折痕把△ADE折起,使点D到达点P的位置(P平面ABCE).
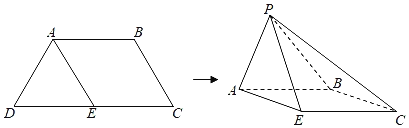
(1)证明:AE⊥PB;
(2)若直线PB与平面ABCE所成的角为![]() ,求二面角A﹣PE﹣C的余弦值.
,求二面角A﹣PE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在首项为-1的等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足
满足
![]() ?若存在,求出
?若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列![]() 是“K数列”,数列
是“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,试判断数列
,试判断数列![]() 是否为“K数列”,并说明理由.
是否为“K数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:

(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“三分损益法”是古代中国发明制定音律时所用的方法,其基本原理是:以一根确定长度的琴弦为基准,取此琴强长度的![]() 得到第二根琴弦,第二根琴弦长度的
得到第二根琴弦,第二根琴弦长度的![]() 为第三根琴弦,第三根琴弦长度的
为第三根琴弦,第三根琴弦长度的![]() 为第四根琴弦.第四根琴弦长度的
为第四根琴弦.第四根琴弦长度的![]() 为第五根琴弦.琴弦越短,发出的声音音调越高,这五根琴弦发出的声音按音调由低到高分别称为“官、商、角(jué)、微(zhǐ)、羽”,则“角"和“徵”对应的琴弦长度之比为( )
为第五根琴弦.琴弦越短,发出的声音音调越高,这五根琴弦发出的声音按音调由低到高分别称为“官、商、角(jué)、微(zhǐ)、羽”,则“角"和“徵”对应的琴弦长度之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() 。
。
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() 左,右顶点分别为
左,右顶点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() ,为椭圆
,为椭圆![]() 上位于
上位于![]() 轴上方的两点,且
轴上方的两点,且![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com