
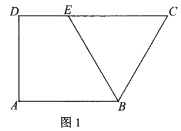
【题目】图1是直角梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .以
.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且
的位置,且![]() ,如图2.
,如图2.
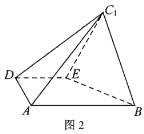
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】下列关于独立性检验的叙述
①常用等高条形图表示列联表数据的频率特征;
②独立性检验依据小概率原理;
③独立性检验的结果是完全正确的;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,
越小,![]() 与
与![]() 有关系的把握程度就越大.
有关系的把握程度就越大.
其中叙述正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查![]() 结果只有“满意”和“不满意”两种
结果只有“满意”和“不满意”两种![]() ,从被调查的学生中随机抽取了50人,具体的调查结果如表:
,从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 的直角梯形,
的直角梯形,![]() ∥BC,
∥BC,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(
上一点(![]() 不与端点重合).
不与端点重合).
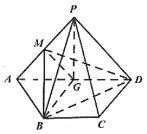
(1)若![]() ,
,
(ⅰ)求证:PC∥平面![]() ;
;
(ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(2)否存在实数![]() 满足
满足![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,若存在,确定的
,若存在,确定的![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知asinB=bsin(A![]() ).
).
(1)求A;
(2)D是线段BC上的点,若AD=BD=2,CD=3,求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com