
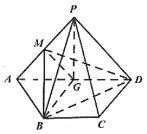
【题目】如图,已知四边形![]() 的直角梯形,
的直角梯形,![]() ∥BC,
∥BC,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点(
上一点(![]() 不与端点重合).
不与端点重合).
(1)若![]() ,
,
(ⅰ)求证:PC∥平面![]() ;
;
(ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(2)否存在实数![]() 满足
满足![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,若存在,确定的
,若存在,确定的![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
【答案】(1)(ⅰ)证明见解析(ⅱ)![]() (2)存在,
(2)存在,![]()
【解析】
(1)(i)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,依题意易证四边形
,依题意易证四边形![]() 为平行四边形,从而有
为平行四边形,从而有![]() ,
,![]() ,由此能证明PC∥平面
,由此能证明PC∥平面![]()
(ii)推导出![]() ,以
,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,利用向量法求解;
,利用向量法求解;
(2)设![]() ,求出平面
,求出平面![]() 的法向量,利用向量法求解.
的法向量,利用向量法求解.
(1)(ⅰ)证明:连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() 为线段
为线段![]() 的中点,
的中点,![]()
所以![]() ,
,
因为![]() ,所以
,所以![]()
因为![]() ∥
∥![]()
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]()
又因为![]() ,
,
所以![]()
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
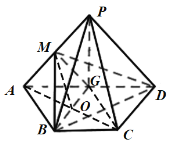
(ⅱ)解:如图,在平行四边形![]() 中
中
因为![]() ,
,![]() ,
,
所以![]()
以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]()
则![]() ,
,![]() ,
,![]() ,
,
![]()
所以![]() ,
,![]() ,
,![]() ,
,![]()
平面![]() 的法向量为
的法向量为![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,即
,即![]() ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 和平面
和平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,则
,则
所以锐二面角的余弦值为![]()
(2)设![]()
所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
 ,取
,取![]() ,得
,得![]() ,
,
因为直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,
,
所以

解得![]()
所以存在![]() 满足
满足![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,
,![]() 为
为![]() 右支上的动点(非顶点),
右支上的动点(非顶点),![]() 为
为![]() 的内心.当
的内心.当![]() 变化时,
变化时,![]() 的轨迹为( )
的轨迹为( )
A.直线的一部分B.椭圆的一部分
C.双曲线的一部分D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最新研究发现,花太多时间玩手机游戏的儿童,患多动症的风险会加倍.青少年的大脑会很快习惯闪烁的屏幕、变幻莫测的手机游戏,一旦如此,他们在教室等视觉刺激较少的地方,就很难集中注意力.研究人员对110名年龄在7岁到8岁的儿童随机调查,并在孩子父母的帮助下记录了他们在1个月里玩手机游戏的习惯.同时,教师记下这些孩子出现的注意力不集中问题.统计得到下列数据:
注意力不集中 | 注意力集中 | 总计 | |
不玩手机游戏 | 20 | 40 | 60 |
玩手机游戏 | 30 | 20 | 50 |
总计 | 50 | 60 | 110 |
(1)试估计7岁到8岁不玩手机游戏的儿童中注意力集中的概率;
(2)能否在犯错误的概率不超过0.010的前提下认为玩手机游戏与注意力集中有关系?
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.840 | 5.024 | 6.635 | 7.879 | td style="width:27.75pt; border-top-style:solid; border-top-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明与另外2名同学进行“手心手背”游戏,规则是:3人同时随机等可能选择手心或手背中的一种手势,规定相同手势人数多者每人得1分,其余每人得0分.现3人共进行了4次游戏,记小明4次游戏得分之和为![]() ,则
,则![]() 的期望为( )
的期望为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.
(1)现有可围![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为![]() ,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
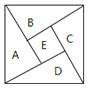
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探月工程“嫦娥四号”探测器于2018年12月8日成功发射,实现了人类首次月球背面软着陆.以嫦娥四号为任务圆满成功为标志,我国探月工程四期和深空探测工程全面拉开序幕.根据部署,我国探月工程到2020年前将实现“绕、落、回”三步走目标.为了实现目标,各科研团队进行积极的备战工作.某科研团队现正准备攻克甲、乙、丙三项新技术,甲、乙、丙三项新技术独立被攻克的概率分别为![]() ,若甲、乙、丙三项新技术被攻克,分别可获得科研经费
,若甲、乙、丙三项新技术被攻克,分别可获得科研经费![]() 万,
万,![]() 万,
万,![]() 万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
(1)求该科研团队获得![]() 万科研经费的概率;
万科研经费的概率;
(2)记该科研团队获得的科研经费为随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网正在改变着人们的生活方式,在日常消费中手机支付正逐渐取代现金支付成为人们首选的支付方式. 某学生在暑期社会活动中针对人们生活中的支付方式进行了调查研究. 采用调查问卷的方式对100名18岁以上的成年人进行了研究,发现共有60人以手机支付作为自己的首选支付方式,在这60人中,45岁以下的占![]() ,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
(1)从以现金作为首选支付方式的40人中,任意选取3人,求这3人至少有1人的年龄低于45岁的概率;
(2)某商家为了鼓励人们使用手机支付,做出以下促销活动:凡是用手机支付的消费者,商品一律打八折. 已知某商品原价50元,以上述调查的支付方式的频率作为消费者购买该商品的支付方式的概率,设销售每件商品的消费者的支付方式都是相互独立的,求销售10件该商品的销售额的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com