【题目】如图为我国数学家赵爽
约3世纪初
在为《周髀算经》作注时验证勾股定理的示意图，现在提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，则
区域涂色不相同的概率为
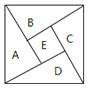
A. 
B. 
C. 
D. 
【答案】B
【解析】
利用分步计数原理求出不同的涂色方案有420种，其中，
区域涂色不相同的情况有120种，由此根据古典概型概率公式能求出区域涂色不相同的概率．
提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，
根据题意，如图，设5个区域依次为
,分4步进行
，对于区域
，有5种颜色可选；
，对于区域
与区域相邻，有4种颜色可选；
，对于区域
，与
区域相邻，有3种颜色可选；
，对于区域
，若
与颜色相同，
区域有3种颜色可选，
若与颜色不相同，区域有2种颜色可选，区域有2种颜色可选，
则区域有
种选择，
则不同的涂色方案有
种，
其中，区域涂色不相同的情况有：
，对于区域，有5种颜色可选；
，对于区域与区域相邻，有4种颜色可选；
，对于区域与
区域相邻，有2种颜色可选；
，对于区域，若与颜色相同，区域有2种颜色可选，
若与颜色不相同，区域有1种颜色可选，区域有1种颜色可选，
则区域有
种选择，
不同的涂色方案有
种，
区域涂色不相同的概率为
,故选B．
天天练口算系列答案科目：高中数学 来源： 题型：
【题目】已知抛物线
的准线与双曲线
相交于
、
两点，双曲线的一条渐近线方程是
，点
是抛物线的焦点，且
是等边三角形，则该双曲线的标准方程是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了美化环境，某公园欲将一块空地规划建成休闲草坪，休闲草坪的形状为如图所示的四边形ABCD．其中AB＝3百米，AD＝
百米，且△BCD是以D为直角顶点的等腰直角三角形．拟修建两条小路AC，BD（路的宽度忽略不计），设∠BAD＝
，
(
，
)．
（1）当cos＝
时，求小路AC的长度；
（2）当草坪ABCD的面积最大时，求此时小路BD的长度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将杨辉三角中的奇数换成1，偶数换成0，便可以得到如图的“0-1三角”.在“
三角”中，从第1行起，设第n
次出现全行为1时，1的个数为
，则
等于（ ）
A.13B.14C.15D.16
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】男运动员6名，女运动员4名，其中男女队长各1名.选派5人外出比赛，在下列情形中各有多少种选派方法？
（1）男运动员3名，女运动员2名；
（2）至少有1名女运动员；
（3）队长中至少有1人参加；
（4）既要有队长，又要有女运动员.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中，随机抽取100名，按年龄(单位:岁）进行统计的频率分布直方图如图：
（1）根据频率分布直方图，分别求出样本的平均数（同一组数据用该区间的中点值作代表)和中位数的估计值(均精确到个位）；
（2）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加华为手机宣传活动，现从这20人中，随机选取2人各赠送一部华为手机，求这2名市民年龄都在
内的人数为
，求的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
，圆
，点
是圆上一动点， 
的垂直平分线与
交于点
.
（1）求点
的轨迹方程；
（2）设点
的轨迹为曲线
，过点
且斜率不为0的直线
与
交于
两点，点
关于
轴的对称点为
，证明直线
过定点，并求
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
