
【题目】已知函数![]() .
.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值并判断
的值并判断![]() 是极大值点还是极小值点;
是极大值点还是极小值点;
![]() Ⅱ
Ⅱ![]() 当函数
当函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() 时,总有
时,总有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() 为极大值点(Ⅱ)
为极大值点(Ⅱ)![]() .
.
【解析】
(Ⅰ)求出函数的导数,求出a的值,得到函数的单调区间,求出函数的极值点即可;
(Ⅱ)求出函数极值点,问题转化为![]() [2lnx1
[2lnx1![]() ]>0,根据0<x1<1时,
]>0,根据0<x1<1时,![]() 0.1<x1<2时,
0.1<x1<2时,![]() 0.即h(x)=2lnx
0.即h(x)=2lnx![]() (0<x<2),通过讨论t的范围求出函数的单调性,从而确定t的范围即可.
(0<x<2),通过讨论t的范围求出函数的单调性,从而确定t的范围即可.
(Ⅰ)![]() ,
,![]() ,则
,则![]()
从而![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
![]() 时,
时,![]() ,
,![]() 为减函数,所以
为减函数,所以![]() 为极大值点.
为极大值点.
(Ⅱ)函数![]() 的定义域为
的定义域为![]() ,有两个极值点
,有两个极值点
![]() ,
,![]() ,则
,则![]() 在
在![]() 上有两个不等的正实根,所以
上有两个不等的正实根,所以![]() ,
,
由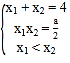 可得
可得![]()
从而问题转化为在![]() ,且
,且![]() 时
时![]() 成立.
成立.
即证![]() 成立.
成立.
即证![]() 即证
即证![]()
亦即证 ![]() . ①
. ①
令![]() 则
则![]()
1)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上为增函数且
上为增函数且![]() ,①式在
,①式在![]() 上不成立.
上不成立.
2)当![]() 时,
时,![]()
若![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上为减函数且
上为减函数且![]() ,
,
![]() 、
、![]() 在区间
在区间![]() 及
及![]() 上同号,故①式成立.
上同号,故①式成立.
若![]() ,即
,即![]() 时,
时,![]() 的对称轴
的对称轴![]() ,
,
令![]() ,则
,则![]() 时,
时,![]() ,不合题意.
,不合题意.
综上可知:![]() 满足题意.
满足题意.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】田忌赛马是![]() 史记
史记![]() 中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等
中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等![]() 于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注
于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注![]() 假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
田忌的马 | 上等马 | 中等马 | 下等马 |
上等马 |
|
| 1 |
中等马 |
|
|
|
下等马 | 0 |
|
|
比赛规则规定:一次比由三场赛马组成,每场由公子和田忌各出一匹马出骞,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
![]() 如果按孙膑的策略比赛一次,求田忌获胜的概率;
如果按孙膑的策略比赛一次,求田忌获胜的概率;
![]() 如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
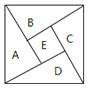
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
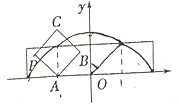
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:①函数
有下列判断:①函数![]() 是偶函数;②对任意的
是偶函数;②对任意的![]() ,都有
,都有![]() ;③函数
;③函数![]() 在区间
在区间![]() 上单调递减;④函数
上单调递减;④函数![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判断正确的序号是__________.
.其中判断正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
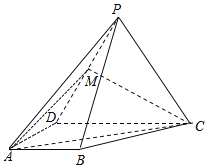
【题目】如图,在四棱锥![]() 中,等边三角形PCD所在的平面垂直于底面ABCD,
中,等边三角形PCD所在的平面垂直于底面ABCD,![]() ,M是棱PD的中点.
,M是棱PD的中点.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面PCD;
平面PCD;
![]() Ⅱ
Ⅱ![]() 求三棱锥
求三棱锥![]() 的体积;
的体积;
![]() Ⅲ
Ⅲ![]() 过B做平面
过B做平面![]() 与平面PAD平行,设平面
与平面PAD平行,设平面![]() 截四棱锥
截四棱锥![]() 所得截面面积为S,试求S的值.
所得截面面积为S,试求S的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.
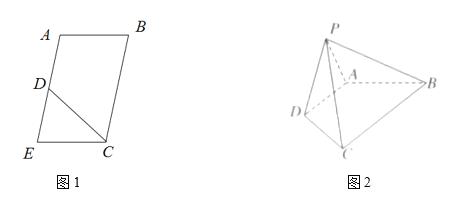
(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市10000名职业中学高三学生参加了一项综合技能测试,从中随机抽取100名学生的测试成绩,制作了以下的测试成绩![]() (满分是184分)的频率分布直方图.
(满分是184分)的频率分布直方图.
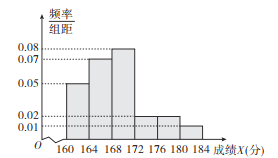
市教育局规定每个学生需要缴考试费100元.某企业根据这100000名职业中学高三学生综合技能测试成绩来招聘员工,划定的招聘录取分数线为172分,且补助已经被录取的学生每个人![]() 元的交通和餐补费.
元的交通和餐补费.
(1)已知甲、乙两名学生的测试成绩分别为168分和170分,求技能测试成绩![]() 的中位数,并对甲、乙的成绩作出客观的评价;
的中位数,并对甲、乙的成绩作出客观的评价;
(2)令![]() 表示每个学生的交费或获得交通和餐补费的代数和,把
表示每个学生的交费或获得交通和餐补费的代数和,把![]() 用
用![]() 的函数来表示,并根据频率分布直方图估计
的函数来表示,并根据频率分布直方图估计![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com