练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列关于独立性检验的叙述

    ①常用等高条形图表示列联表数据的频率特征；

    ②独立性检验依据小概率原理；

    ③独立性检验的结果是完全正确的；

    ④对分类变量与的随机变量的观测值来说，越小，与有关系的把握程度就越大.

    其中叙述正确的个数为（ ）

    A.1B.2C.3D.4

    【答案】B

    【解析】

    由独立性检验常用等髙条形图表示列联表数据的频率特征知①正确，由独立性检验依据的是小概率原理知②正确，由独立性检验的结果是不完全正确的知③不正确，④中应是越大，与有关系的把握程度就越大.

    因为独立性检验常用等髙条形图表示列联表数据的频率特征，故①正确；

    独立性检验依据的是小概率原理，故②正确；

    独立性检验的结果是不完全正确的，故③不正确；

    对分类变量与的随机变量的观测值来说，越大，

    与有关系的把握程度才越大，故④不正确.

    所以正确的个数为2

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2019年“两会”报告指出，5G在下半年会零星推出，2020年有望实现大范围使用。随着移动通信产业的发展，全球移动宽带（，简称）用户数已达54亿，占比70%（用户比例简称渗透率），但在部分发展中国家该比例甚至低于20%。

    基站覆盖率小于80%

    基站覆盖率大于80%

    总计

    渗透率低于20%

    渗透率高于20%

    总计

    （1）现对140个发展中国家进行调查，发现140个发展中国家中有25个国家MBB基站覆盖率小于80%，其中渗透率低于20%的有15个国家，而基站覆盖率大于80%的国家中渗透率低于20%的有25个国家.由以上统计数据完成下面列联表，并判断是否有99%的把握认为渗透率与基站覆盖率有关；

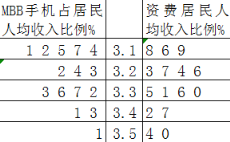
    （2）基站覆盖率小于80%，其中渗透率低于20%的国家中手机占居民人均收入比例和资费居民人均收入比例如茎叶图所示，请根据茎叶图求这些国家中的手机占居民人均收入比例的中位数和资费居民人均收入比例平均数；

    （3）根据以上数据判断，若要提升渗透率，消除数字化鸿沟，把数字世界带入每个人，需要重点解决哪些问题。

    附：参考公式：；其中．

    临界值表：

    0.050

    0.025

    0.010

    0.005

    0.001

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】双曲线的左、右焦点为，，为右支上的动点（非顶点），为的内心.当变化时，的轨迹为（ ）

    A.直线的一部分B.椭圆的一部分

    C.双曲线的一部分D.无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在菱形中，，平面平面是线段的中点，.

    （1）证明：平面.

    （2）求直线与平面所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入,则输出的结果是( )

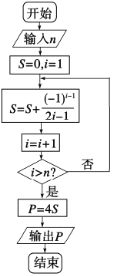
    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是等差数列，其前项中的奇数项的和与偶数项的和之差为.

    （1）请证明这一结论对任意等差数列（中各项均不为零）恒成立；

    （2）请类比等差数列的结论，对于各项均为正数的等比数列，提出猜想，并加以证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】最新研究发现，花太多时间玩手机游戏的儿童，患多动症的风险会加倍．青少年的大脑会很快习惯闪烁的屏幕、变幻莫测的手机游戏，一旦如此，他们在教室等视觉刺激较少的地方，就很难集中注意力．研究人员对110名年龄在7岁到8岁的儿童随机调查，并在孩子父母的帮助下记录了他们在1个月里玩手机游戏的习惯．同时，教师记下这些孩子出现的注意力不集中问题．统计得到下列数据：

    注意力不集中

    注意力集中

    总计

    不玩手机游戏

    20

    40

    60

    玩手机游戏

    30

    20

    50

    总计

    50

    60

    110

    （1）试估计7岁到8岁不玩手机游戏的儿童中注意力集中的概率；

    （2）能否在犯错误的概率不超过0.010的前提下认为玩手机游戏与注意力集中有关系？

    附表：

    td style="width:27.75pt; border-top-style:solid; border-top-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">

    10.828

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.840

    5.024

    6.635

    7.879

    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】图1是直角梯形，，，，，，.以为折痕将折起，使点到达的位置，且，如图2.

    （1）证明：平面平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】探月工程“嫦娥四号”探测器于2018年12月8日成功发射，实现了人类首次月球背面软着陆.以嫦娥四号为任务圆满成功为标志，我国探月工程四期和深空探测工程全面拉开序幕.根据部署，我国探月工程到2020年前将实现“绕、落、回”三步走目标.为了实现目标，各科研团队进行积极的备战工作.某科研团队现正准备攻克甲、乙、丙三项新技术，甲、乙、丙三项新技术独立被攻克的概率分别为，若甲、乙、丙三项新技术被攻克，分别可获得科研经费万，万，万.若其中某项新技术未被攻克，则该项新技术没有对应的科研经费.

    （1）求该科研团队获得万科研经费的概率；

    （2）记该科研团队获得的科研经费为随机变量，求的分布列与数学期望.

    查看答案和解析>>

    同步练习册答案