练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知是等差数列，其前项中的奇数项的和与偶数项的和之差为.

    （1）请证明这一结论对任意等差数列（中各项均不为零）恒成立；

    （2）请类比等差数列的结论，对于各项均为正数的等比数列，提出猜想，并加以证明.

    【答案】（1）证明见解析（2）类比猜想：各项均为正数的等比数列的前项中奇数项的积与偶数项的积的比为，证明见解析

    【解析】

    （1）由，可得

    （2）类比猜想可得：各项均为正数的等比数列的前项中奇数项的积与偶数项的积的比为，然后证明出来即可.

    证明：（1）记为等差数列前项中奇数项的和，

    为等差数列前项中偶数项的和，

    由等差数列的前项和公式可得，

    ，

    .

    命题成立.

    （2）解：类比猜想可得：各项均为正数的等比数列的前项中奇数项的积与偶数项的积的比为.

    证明：记各项均为正数的等比数列的前项中奇数项的积为，

    偶数项的积为，

    ，即，

    ，即，

    ，即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某省积极响应教育部号召实行新课程改革，为了调查某校高三学生的物理考试成绩是否达到级与学生性别是否有关，从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表：

    考试成绩达到级

    考试成绩未达到级

    总计

    男生

    26

    40

    女生

    6

    总计

    70

    （1）（ⅰ）将列联表补充完整；

    （ⅱ）据此列联表判断，能否有的把握认为“物理考试成绩是否达到级与性别有关”？

    （2）将频率视作概率，从该校高三年级任意抽取3名学生的成绩，求物理考试成绩达到级的人数的分布列及期望．

    附：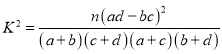

    0.050

    0.010

    0.001

    3.841

    6.635

    10..828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校开设了射击选修课，规定向、两个靶进行射击：先向靶射击一次，命中得1分，没有命中得0分，向靶连续射击两次，每命中一次得2分，没命中得0分；小明同学经训练可知：向靶射击，命中的概率为，向靶射击，命中的概率为，假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.

    （1）求小明同学恰好命中一次的概率；

    （2）求小明同学获得总分的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的短轴长为，离心率，其右焦点为.

    （1）求椭圆的方程；

    （2）过作夹角为的两条直线分别交椭圆于和，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于独立性检验的叙述

    ①常用等高条形图表示列联表数据的频率特征；

    ②独立性检验依据小概率原理；

    ③独立性检验的结果是完全正确的；

    ④对分类变量与的随机变量的观测值来说，越小，与有关系的把握程度就越大.

    其中叙述正确的个数为（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有如下命题，其中真命题的标号为（ ）

    A.若幂函数的图象过点，则

    B.函数（，且）的图象恒过定点

    C.函数有两个零点

    D.若函数在区间上的最大值为4，最小值为3，则实数m的取值范围是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合，是非空集合的两个不同子集.

    （1）若，且是的子集，求所有有序集合对的个数；

    （2）若，且是的子集，求所有有序集合对的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某届奥运会上，中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二，某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查结果只有“满意”和“不满意”两种，从被调查的学生中随机抽取了50人，具体的调查结果如表：

    班号

    一班

    二班

    三班

    四班

    五班

    六班

    频数

    5

    9

    11

    9

    7

    9

    满意人数

    4

    7

    8

    5

    6

    6

    （1）在高三年级全体学生中随机抽取一名学生，由以上统计数据估计该生持满意态度的概率；

    （2）若从一班至二班的调查对象中随机选取4人进行追踪调查，记选中的4人中对“本届奥运会中国队表现”不满意的人数为，求随机变量的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为检验两条生产线的优品率，现从两条生产线上各抽取件产品进行检测评分，用茎叶图的形式记录，并规定高于分为优品.前件的评分记录如下，第件暂不公布.

    （1）求所抽取的生产线上的个产品的总分小于生产线上的第个产品的总分的概率；

    （2）已知生产线的第件产品的评分分别为.

    ①从生产线的件产品里面随机抽取件，设非优品的件数为，求的分布列和数学期望；

    ②以所抽取的样本优品率来估计生产线的优品率，从生产线上随机抽取件产品，记优品的件数为，求的数学期望.

    查看答案和解析>>

    同步练习册答案