练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入,则输出的结果是( )

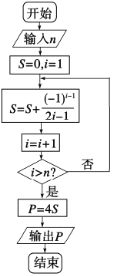
    A.B.

    C.D.

    【答案】B

    【解析】

    执行给定的程序框图，输入，逐次循环，找到计算的规律，即可求解.

    由题意，执行给定的程序框图，输入，可得：

    第1次循环：；

    第2次循环：；

    第3次循环：；

    第10次循环：，

    此时满足判定条件，输出结果，

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市垃圾处理厂的垃圾年处理量（单位：千万吨）与资金投入量x（单位：千万元）有如下统计数据：

    2012年

    2013年

    2014年

    2015年

    2016年

    资金投入量x（千万元）

    1.5

    1.4

    1.9

    1.6

    2.1

    垃圾处理量y（千万吨）

    7.4

    7.0

    9.2

    7.9

    10.0

    （1）若从统计的5年中任取2年，求这2年的垃圾处理量至少有一年不低于8.0（千万吨）的概率；

    （2）由表中数据求得线性回归方程为，该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨，现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元，请你预测2017年能否完成垃圾处理任务，若不能，缺口约为多少千万吨？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且满足，，设，则以下四个命题：（1）是等差数列；（2）中最大项是；（3）通项公式是；（4）.其中真命题的序号是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，求函数的单调区间；

    （2）若不等式对任意的正实数都成立，求实数的最大整数值.

    （3）当时，若存在实数且，使得，求证.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）求函数的单调区间；

    （Ⅲ）若对任意的，都有成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于独立性检验的叙述

    ①常用等高条形图表示列联表数据的频率特征；

    ②独立性检验依据小概率原理；

    ③独立性检验的结果是完全正确的；

    ④对分类变量与的随机变量的观测值来说，越小，与有关系的把握程度就越大.

    其中叙述正确的个数为（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面是边长为2的菱形，是的中点．

    （1）证明：平面；

    （2）设是线段上的动点，当点到平面距离最大时，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角梯形中，，，，，是的中点，是与的交点．将沿折起到的位置，如图．

    （Ⅰ）证明：平面；

    （Ⅱ）若平面平面，求平面与平面夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】自2017年起，部分省、市陆续实施了新高考，某省采用了“”的选科模式，即：考试除必考的语、数、外三科外，再从物理、化学、生物、历史、地理、政治六个学科中，任意选取三科参加高考，为了调查新高考中考生的选科情况，某地区调查小组进行了一次调查，研究考生选择化学与选择物理是否有关.已知在调查数据中，选物理的考生与不选物理的考生人数相同，其中选物理且选化学的人数占选物理人数的，在不选物理的考生中，选化学与不选化学的人数比为.

    （1）若在此次调查中，选物理未选化学的考生有100人，试完成下面的列联表：

    选化学

    不选化学

    合计（人数）

    选物理

    不选物理

    合计（人数）

    （2）根据第（1）问的数据，能否有99%把握认为选择化学与选择物理有关？

    （3）若研究得到在犯错误概率不超过0.01的前提下，认为选化学与选物理有关，则选物理又选化学的人数至少有多少？（单位：千人；精确到0.001）

    附：.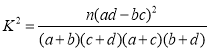

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    同步练习册答案