
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,则以下四个命题:(1)
,则以下四个命题:(1)![]() 是等差数列;(2)
是等差数列;(2)![]() 中最大项是
中最大项是![]() ;(3)
;(3)![]() 通项公式是
通项公式是![]() ;(4)
;(4)![]() .其中真命题的序号是______.
.其中真命题的序号是______.
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(2sin x,
=(2sin x,![]() cos x),
cos x),![]() =(-sin x,2sin x),函数f(x)=
=(-sin x,2sin x),函数f(x)=![]() ·
·![]()
(1)求f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=1,c=1,ab=2![]() ,且a>b,求a,b的值.
,且a>b,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() ,
,![]() ,给出下列曲线方程:(1)
,给出下列曲线方程:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,在曲线上存在点
,在曲线上存在点![]() 满足
满足![]() 的所有曲线是( )
的所有曲线是( )
A.(1)(2)(3)(4)B.(2)(3)
C.(1)(4)D.(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足:①对于任意的正整数
同时满足:①对于任意的正整数![]() ,
, ![]() 恒成立;②对于给定的正整数
恒成立;②对于给定的正整数![]() ,
, ![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,则称数列
恒成立,则称数列![]() 是“
是“![]() 数列”.
数列”.
(1)已知![]() 判断数列
判断数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(2)已知数列![]() 是“
是“![]() 数列”,且存在整数
数列”,且存在整数![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,证明:
成等差数列,证明: ![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了50人就该城市共享单车的推行情况进行问卷调査,并将问卷中的这50人根据其满意度评分值(百分制)按照![]() 分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
分成5组,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
频率分布表
组别 | 分组 | 频数 | 频率 |
第1组 |
| 8 | 0.16 |
第2组 |
|
| ▆ |
第3组 |
| 20 | 0.40 |
第4组 |
| ▆ | 0.08 |
第5组 |
| 2 |
|
合计 | ▆ | ▆ |
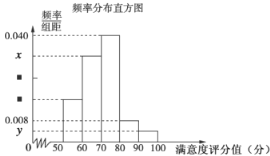
(1)求![]() 的值;
的值;
(2)若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
的人中随机抽取2人进行座谈,求所抽取的2人中至少一人来自第5组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com