
【题目】自2017年起,部分省、市陆续实施了新高考,某省采用了“![]() ”的选科模式,即:考试除必考的语、数、外三科外,再从物理、化学、生物、历史、地理、政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地区调查小组进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的
”的选科模式,即:考试除必考的语、数、外三科外,再从物理、化学、生物、历史、地理、政治六个学科中,任意选取三科参加高考,为了调查新高考中考生的选科情况,某地区调查小组进行了一次调查,研究考生选择化学与选择物理是否有关.已知在调查数据中,选物理的考生与不选物理的考生人数相同,其中选物理且选化学的人数占选物理人数的![]() ,在不选物理的考生中,选化学与不选化学的人数比为
,在不选物理的考生中,选化学与不选化学的人数比为![]() .
.
(1)若在此次调查中,选物理未选化学的考生有100人,试完成下面的列联表:
选化学 | 不选化学 | 合计(人数) | |
选物理 | |||
不选物理 | |||
合计(人数) |
(2)根据第(1)问的数据,能否有99%把握认为选择化学与选择物理有关?
(3)若研究得到在犯错误概率不超过0.01的前提下,认为选化学与选物理有关,则选物理又选化学的人数至少有多少?(单位:千人;精确到0.001)
附: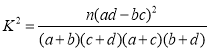 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)列联表详见解析(2)有99%把握认为选择化学与选择物理有关(3)至少有11.943千人
【解析】
(1)根据题意,即可求得表格中缺失的数据;
(2)结合列联表,计算![]() ,即可进行判断;
,即可进行判断;
(3)设选物理又选化学的人数为![]() 千人,据此重新求得列联表,以及
千人,据此重新求得列联表,以及![]() ,根据其大于等于
,根据其大于等于![]() ,即可求得结果.
,即可求得结果.
(1)列联表如下:
选化学 | 不选化学 | 合计(人数) | |
选物理 | 150 | 100 | 250 |
不选物理 | 50 | 200 | 250 |
合计(人数) | 200 | 300 | 500 |
(2)由列联表可知![]() ,
,
所以有99%把握认为选择化学与选择物理有关.
(3)设选物理又选化学的人数为![]() 千人,则列联表如下:
千人,则列联表如下:
选化学 | 不选化学 | 合计(人数) | |
选物理 |
|
|
|
不选物理 |
|
|
|
合计(人数) |
|
|
|
所以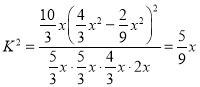 ,
,
在犯错误概率不超过0.01的前提下,则![]() ,即
,即![]() ,解得
,解得![]() (千人),所以选物理又选化学的人数至少有11.943千人.
(千人),所以选物理又选化学的人数至少有11.943千人.


科目:高中数学 来源: 题型:
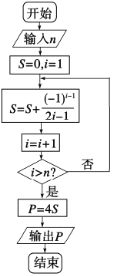
【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入![]() ,则输出的结果是( )
,则输出的结果是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明与另外2名同学进行“手心手背”游戏,规则是:3人同时随机等可能选择手心或手背中的一种手势,规定相同手势人数多者每人得1分,其余每人得0分.现3人共进行了4次游戏,记小明4次游戏得分之和为![]() ,则
,则![]() 的期望为( )
的期望为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
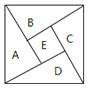
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn,且an2+2an=4Sn﹣1(n∈N*).
(1)求数列{an}的通项公式;
(2)若bn![]() ,数列{bn}的前n项和为Tn,求Tn的取值范围.
,数列{bn}的前n项和为Tn,求Tn的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探月工程“嫦娥四号”探测器于2018年12月8日成功发射,实现了人类首次月球背面软着陆.以嫦娥四号为任务圆满成功为标志,我国探月工程四期和深空探测工程全面拉开序幕.根据部署,我国探月工程到2020年前将实现“绕、落、回”三步走目标.为了实现目标,各科研团队进行积极的备战工作.某科研团队现正准备攻克甲、乙、丙三项新技术,甲、乙、丙三项新技术独立被攻克的概率分别为![]() ,若甲、乙、丙三项新技术被攻克,分别可获得科研经费
,若甲、乙、丙三项新技术被攻克,分别可获得科研经费![]() 万,
万,![]() 万,
万,![]() 万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
(1)求该科研团队获得![]() 万科研经费的概率;
万科研经费的概率;
(2)记该科研团队获得的科研经费为随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有6个学生餐厅,甲、乙、丙、丁四位同学每人随机地选择一家餐厅就餐(选择到每个餐厅概率相同),则下列结论正确的是( )
A.四人去了四个不同餐厅就餐的概率为![]()
B.四人去了同一餐厅就餐的概率为![]()
C.四人中恰有2人去了第一餐厅就餐的概率为![]()
D.四人中去第一餐厅就餐的人数的期望为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com