
【题目】2019年“两会”报告指出,5G在下半年会零星推出,2020年有望实现大范围使用。随着移动通信产业的发展,全球移动宽带(![]() ,简称
,简称![]() )用户数已达54亿,占比70%(
)用户数已达54亿,占比70%(![]() 用户比例简称
用户比例简称![]() 渗透率),但在部分发展中国家该比例甚至低于20%。
渗透率),但在部分发展中国家该比例甚至低于20%。
|
| 总计 | |
| |||
| |||
总计 |
(1)现对140个发展中国家进行调查,发现140个发展中国家中有25个国家MBB基站覆盖率小于80%,其中![]() 渗透率低于20%的有15个国家,而
渗透率低于20%的有15个国家,而![]() 基站覆盖率大于80%的国家中
基站覆盖率大于80%的国家中![]() 渗透率低于20%的有25个国家.由以上统计数据完成下面
渗透率低于20%的有25个国家.由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为
列联表,并判断是否有99%的把握认为![]() 渗透率与
渗透率与![]() 基站覆盖率有关;
基站覆盖率有关;
(2)![]() 基站覆盖率小于80%,其中
基站覆盖率小于80%,其中![]() 渗透率低于20%的国家中
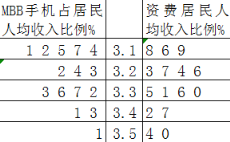
渗透率低于20%的国家中![]() 手机占居民人均收入比例和资费居民人均收入比例如茎叶图所示,请根据茎叶图求这些国家中的
手机占居民人均收入比例和资费居民人均收入比例如茎叶图所示,请根据茎叶图求这些国家中的![]() 手机占居民人均收入比例的中位数和资费居民人均收入比例平均数;
手机占居民人均收入比例的中位数和资费居民人均收入比例平均数;
(3)根据以上数据判断,若要提升![]() 渗透率,消除数字化鸿沟,把数字世界带入每个人,需要重点解决哪些问题。
渗透率,消除数字化鸿沟,把数字世界带入每个人,需要重点解决哪些问题。
附:参考公式:![]() ;其中
;其中![]() .
.
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)见解析;(2)中位数是3.24%;平均数约为3.32%;(3)见解析
【解析】
(1)完善列联表,再计算![]() ,然后与临界值表作比较得到答案.
,然后与临界值表作比较得到答案.
(2)![]() 手机占居民人均收入比例一共是15个数据,第8个数据为中位数,利用平均值公式得到答案.
手机占居民人均收入比例一共是15个数据,第8个数据为中位数,利用平均值公式得到答案.
(3)需要重点解决手机贵、资费高和基站覆盖低的问题.
解:(1)
|
| 总计 | |
| 15 | 25 | 40 |
| 10 | 90 | 100 |
总计 | 25 | 115 | 140 |
![]()
所以有99%的把握认为![]() 渗透率与
渗透率与![]() 基站覆盖率有关
基站覆盖率有关
(2)![]() 手机占居民人均收入比例一共是15个数据,第8个数据为3.24%,所以中位数是3.24%;
手机占居民人均收入比例一共是15个数据,第8个数据为3.24%,所以中位数是3.24%;
![]() 资费居民人均收入比例平均数约为:3.32%
资费居民人均收入比例平均数约为:3.32%
(3)根据以上数据判断, ![]() 用户发展受限的因素分别是手机、资费、基站覆盖,若要提升
用户发展受限的因素分别是手机、资费、基站覆盖,若要提升![]() 渗透率,消除数字化鸿沟,把数字世界带入每个人,需要重点解决手机贵、资费高和基站覆盖低的问题.
渗透率,消除数字化鸿沟,把数字世界带入每个人,需要重点解决手机贵、资费高和基站覆盖低的问题.


科目:高中数学 来源: 题型:
【题目】盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球.规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得![]() 分,现从盒内任取3个球.
分,现从盒内任取3个球.
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为![]() .
.
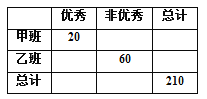
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附: 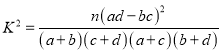
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理厂的垃圾年处理量(单位:千万吨)与资金投入量x(单位:千万元)有如下统计数据:
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
资金投入量x(千万元) | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾处理量y(千万吨) | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
(1)若从统计的5年中任取2年,求这2年的垃圾处理量至少有一年不低于8.0(千万吨)的概率;
(2)由表中数据求得线性回归方程为![]() ,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省积极响应教育部号召实行新课程改革,为了调查某校高三学生的物理考试成绩是否达到![]() 级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
考试成绩达到 | 考试成绩未达到 | 总计 | |
男生 | 26 | 40 | |
女生 | 6 | ||
总计 | 70 |
(1)(ⅰ)将![]() 列联表补充完整;
列联表补充完整;
(ⅱ)据此列联表判断,能否有![]() 的把握认为“物理考试成绩是否达到级与性别有关”?
的把握认为“物理考试成绩是否达到级与性别有关”?
(2)将频率视作概率,从该校高三年级任意抽取3名学生的成绩,求物理考试成绩达到![]() 级的人数的分布列及期望.
级的人数的分布列及期望.
附: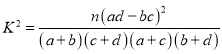
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于独立性检验的叙述
①常用等高条形图表示列联表数据的频率特征;
②独立性检验依据小概率原理;
③独立性检验的结果是完全正确的;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,
越小,![]() 与
与![]() 有关系的把握程度就越大.
有关系的把握程度就越大.
其中叙述正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com