
分析 (1)当n≥2时通过2an-Sn=1与2an-1-Sn-1=1作差,进而计算可得结论;
(2)通过(1)可得Tn的表达式,进而计算即得结论;
(3)通过(1)可知数列{cn}的通项公式,利用并项相加、分n为奇数、偶数两种情况讨论即可.
解答 (1)证明:∵2an-Sn=1,
∴当n≥2时,2an-1-Sn-1=1,
两式相减,整理得:an=2an-1(n≥2),
又∵2a1-S1=1,即a1=1,
∴数列{an}是首项为1、公比为2的等比数列,
∴an=2n-1;
(2)解:∵Tn=(1+2+22+…+2n-1)(1+2+22+…+2n-1)
=$\frac{1-{2}^{n}}{1-2}$•$\frac{1-{2}^{n}}{1-2}$
=4n-2•2n+1,
∴$\lim_{x→∞}\frac{T_n}{4^n}$=$\underset{lim}{x→∞}$$\frac{{4}^{n}-2•{2}^{n}+1}{{4}^{n}}$=1;
(3)结论:存在这样的实数t,使得对于所有的n都有${C_n}≥t{n^2}$成立.
理由如下:
由(1)可知,1+bn=3log2an=3n-3,即bn=3n-4,bn+1=3n-1,
故cn=(-1)n+1bn•bn+1=(-1)n+1(3n-4)(3n-1),cn+1=(-1)n+2(3n-1)(3n+2),
特别地,当n为奇数时,有n+1为偶数,
此时cn+cn+1=(3n-4)(3n-1)-(3n-1)(3n+2)=-6(3n-1),
①若n为偶数,则Cn=(c1+c2)+(c3+c4)+…+(cn-1+cn)
=-6×[2+8+…+(3n-4)]
=-$\frac{3}{2}$n(3n-2),
由${C_n}≥t{n^2}$可知t≤-$\frac{3}{2}$(3-$\frac{2}{n}$)对所有正偶数n都成立,故t≤-$\frac{9}{2}$;
②若n为奇数,则Cn=Cn-1+cn(n≥2),
由①可知Cn=-$\frac{3}{2}$(n-1)(3n-5)+(3n-4)(3n-1)=$\frac{9}{2}$n2-3n-$\frac{7}{2}$,
其中C1=-2满足上式;
由①②可得实数t的取值范围是:t≤-$\frac{9}{2}$,
所以存在这样的实数t,使得对于所有的n都有${C_n}≥t{n^2}$成立.
点评 本题是一道关于数列与不等式的综合题,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是PA,PD,AB的中点.
如图,四棱锥P-ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是PA,PD,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PCD⊥底面ABCD,PD⊥CD,PD=CD,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PCD⊥底面ABCD,PD⊥CD,PD=CD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
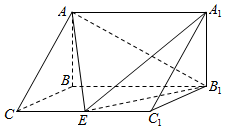 如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=90°,AB⊥侧面BB1C1C,E为CC1的中点
如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=90°,AB⊥侧面BB1C1C,E为CC1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
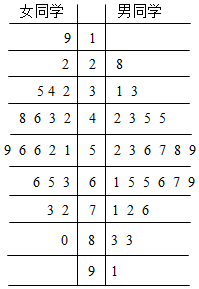 某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数.说明:如图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类
某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数.说明:如图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类| 喜食蔬菜 | 喜食肉类 | 合计 | |
| 男同学 | |||
| 女同学 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com