练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．若复数z=i（1-2i）（i为虚数单位），则$\overline{z}$=（　　）
    A．1-2iB．1+2iC．2+iD．2-i

    分析 利用复数的运算法则、共轭复数的定义即可得出．

    解答 解：复数z=i（1-2i）=i+2，则$\overline{z}$=2-i．
    故选：D．

    点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．运行如图所示的程序框图，则输出的S的值为（　　）
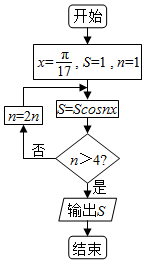
    A．$\frac{1}{4}$B．$\frac{1}{8}$C．$\frac{1}{16}$D．$\frac{1}{32}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某校对高三部分学生的数学质检成绩作相对分析．

    （1）按一定比例进行分层抽样抽取了20名学生的数学成绩，并用茎叶图（图1）记录，但部分数据不小心丢失了，已知数学成绩[70，90）的频率是0.2，请补全表格并绘制相应频率分布直方图（图2）．
     分数段（分）[50，70）[70，90）[90，110）[110，130）[130，150）
     $\frac{频率}{组距}$ 
    0.005    		 
    0.010    		 
    0.020    		 
    0.010    		 
    0.005
    （2）为考察学生的物理成绩与数学成绩是否有关系，抽取了部分同学的数学成绩与物理成绩进行比较，得到统计数据如表：
      物理成绩优秀 物理成绩一般合计 
     数学成绩优秀 15 3 18
     数学成绩一般 5 17 22
     合计 2020 40 
    能够有多大的把握，认为物理成绩优秀与数学成绩优秀有关系？
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
     P（K2≥K0） 0.05 0.01 0.005 0.001
     K0 3.481 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．某班生活委员为了解在春天本班同学感冒与性别是否相关，他收集了3月份本班同学的感冒数据，并制出下面一个2×2列联表：
    感冒不感冒合计
    男生52732
    女生91928
    合计134760
    参考数据
    P（K2≥2.072）≈0.15
    P（K2≥2.706）≈0.10
    P（K2≥6.635）≈0.010
    由K2的观测值公式，可求得k=2.278，根据给出表格信息和参考数据，下面判断正确的是（　　）
    A．在犯错概率不超过10%的前提下认为该班“感冒与性别有关”
    B．在犯错概率不超过10%的前提下不能认为该班“感冒与性别有关”
    C．有15%的把握认为该班“感冒与性别有关”
    D．在犯错概率不超过10%的前提下认为该班“感冒与性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知等差数列{an}的前n项和为Sn=-n2+4n，则其公差d=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若随机变量X的分布列为P（X=i）=$\frac{i}{10}$（i=1，2，3，4），则P（X＞2）=0.7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知n∈N*，数列{an}的前n项和为Sn，且2an-Sn=1．
    （1）求证：数列{an}是等比数列，并求出通项公式；
    （2）对于任意ai、aj∈{a1，a2，…，an}（其中1≤i≤n，1≤j≤n，i、j均为正整数），若ai和aj的所有乘积ai•aj的和记为Tn，试求$\lim_{x→∞}\frac{T_n}{4^n}$的值；
    （3）设$1+{b_n}=3{log_2}{a_n}，{c_n}={（{-1}）^{n+1}}{b_n}•{b_{n+1}}$，若数列{cn}的前n项和为Cn，是否存在这样的实数t，使得对于所有的n都有${C_n}≥t{n^2}$成立，若存在，求出t的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知ABCD-A1B1C1D1为正方体，则二面角B-A1C1-A的余弦值为（　　）
    A．$\frac{\sqrt{2}}{3}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{6}}{3}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．甲、乙两所学校进行同一门课程的考试，按照学生考试成绩优秀和不优秀统计成绩后，得到如下2×2列联表：
    班级与成绩列联表
    优秀不优秀总计
    甲队8040120
    乙队240200440
    合计320240560
    （Ⅰ）能否在犯错误的概率不超过0.025的前提下认为成绩与学校有关系；
    （Ⅱ）采用分层抽样的方法在两所学校成绩优秀的320名学生中抽取16名同学．现从这16名同学中随机抽取3名运同学作为成绩优秀学生代表介绍学习经验，记这3名同学来自甲学校的人数为X，求X的分布列与数学期望．附：
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d）

    查看答案和解析>>

    同步练习册答案