
| 优秀 | 不优秀 | 总计 | |
| 甲队 | 80 | 40 | 120 |
| 乙队 | 240 | 200 | 440 |
| 合计 | 320 | 240 | 560 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)根据列联表做出观测值,把观测值同临界值进行比较,得到有能在犯错误的概率不超过0.025的前提下认为成绩与所在学校有关系;
(Ⅱ)确定ξX的取值,求出相应的概率,可得分布列和数学期望.
解答 解:(Ⅰ)由题意得K2=$\frac{560×(80×200-40×240)^{2}}{120×440×320×240}$≈5.657>5.024,
∴能在犯错误的概率不超过0.025的前提下认为成绩与所在学校有关系.…(3分)
(Ⅱ)16名同学中有甲学校有4人,乙学校有12人…..…(4分)
X的可能取值为0,1,2,3…..…(5分)
P(X=0)=$\frac{{C}_{12}^{3}}{{C}_{16}^{3}}$=$\frac{11}{28}$,P(X=1)=$\frac{{C}_{12}^{2}{C}_{4}^{1}}{{C}_{16}^{3}}$=$\frac{33}{70}$,P(X=2)=$\frac{{C}_{12}^{1}{C}_{4}^{2}}{{C}_{16}^{3}}$=$\frac{9}{70}$,P(X=3)=$\frac{{C}_{4}^{3}}{{C}_{16}^{3}}$=$\frac{1}{140}$
X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{11}{28}$ | $\frac{33}{70}$ | $\frac{9}{70}$ | $\frac{1}{140}$ |
点评 本题主要考查独立性检验的应用,考查离散型随机变量的分布列与期望,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
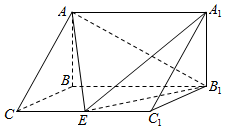 如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=90°,AB⊥侧面BB1C1C,E为CC1的中点
如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=90°,AB⊥侧面BB1C1C,E为CC1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
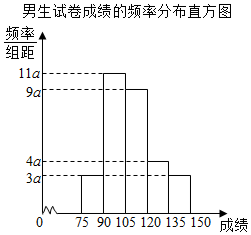 某中学共有4400名学生,其中男生共有2400名,女生2000名,为了解学生的数学基础的差异,采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查,得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表.
某中学共有4400名学生,其中男生共有2400名,女生2000名,为了解学生的数学基础的差异,采用分层抽样的办法从全体学生中选取55名同学进行试卷成绩调查,得到男生试卷成绩的频率分布直方图和女生试卷成绩的频数分布表.| 成绩分组 | [75,90) | [90,105) | [105,120) | [120,135) | [135,150) |
| 频数 | 2 | 6 | 8 | 7 | b |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 不优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| K0 | 2.706 | 3.841 | 6,635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
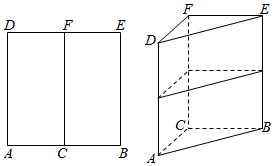
| A. | 16π | B. | 32π | C. | 8π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
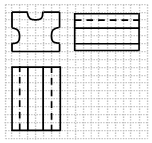
| A. | 240-24π | B. | 240-12π | C. | 240-8π | D. | 240-4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
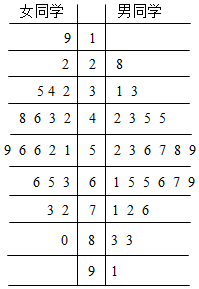 某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数.说明:如图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类
某课题组对全班45名同学的饮食习惯进行了一次调查,并用茎叶图表示45名同学的饮食指数.说明:如图中饮食指数低于70的人被认为喜食蔬菜,饮食指数不低于70的人被认为喜食肉类| 喜食蔬菜 | 喜食肉类 | 合计 | |
| 男同学 | |||
| 女同学 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某组合体的三视图如图示,则该组合体的表面积为( )
某组合体的三视图如图示,则该组合体的表面积为( )| A. | $(6+2\sqrt{2})π+12$ | B. | 8(π+1) | C. | 4(2π+1) | D. | $(12+2\sqrt{2})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,$\frac{1}{4}}$) | C. | (${\frac{1}{4}$,+∞) | D. | (0,$\frac{1}{4}}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com